llvm-学习（六）代码优化方式等


阅读数: 次   

学习资料 （哈工大编译原理）https://www.bilibili.com/video/BV1zW411t7YE?p=62

常用的优化方法

  1. 删除公共子表达式
  2. 删除无用代码
  3. 常量合并
  4. 代码移动
  5. 强度削弱
  6. 删除归纳变量

删除公告子表达式

公共子表达式

如果表达式x op y先前已被计算过，并且从先前的计 算到现在，x op y中变量的值没有改变，那么x op y的

这次出现就称为公共子表达式(common subexpression)

对于这种 公告表达式

又分为：局部公共表达式，全局公共表达式

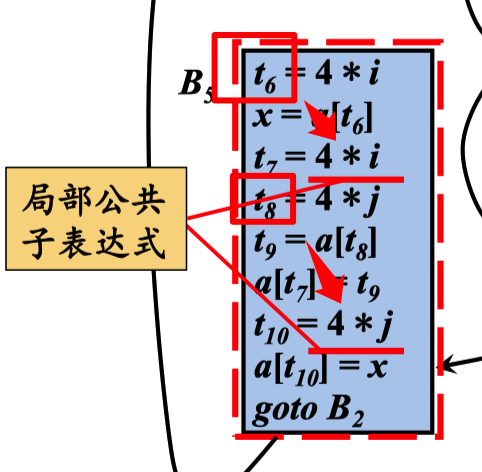
局部公共表达式：指在一个 基本块中，重复定义的。

image-20200717194230732

全局公共表达式：在流图中，上下基本块中 重复的

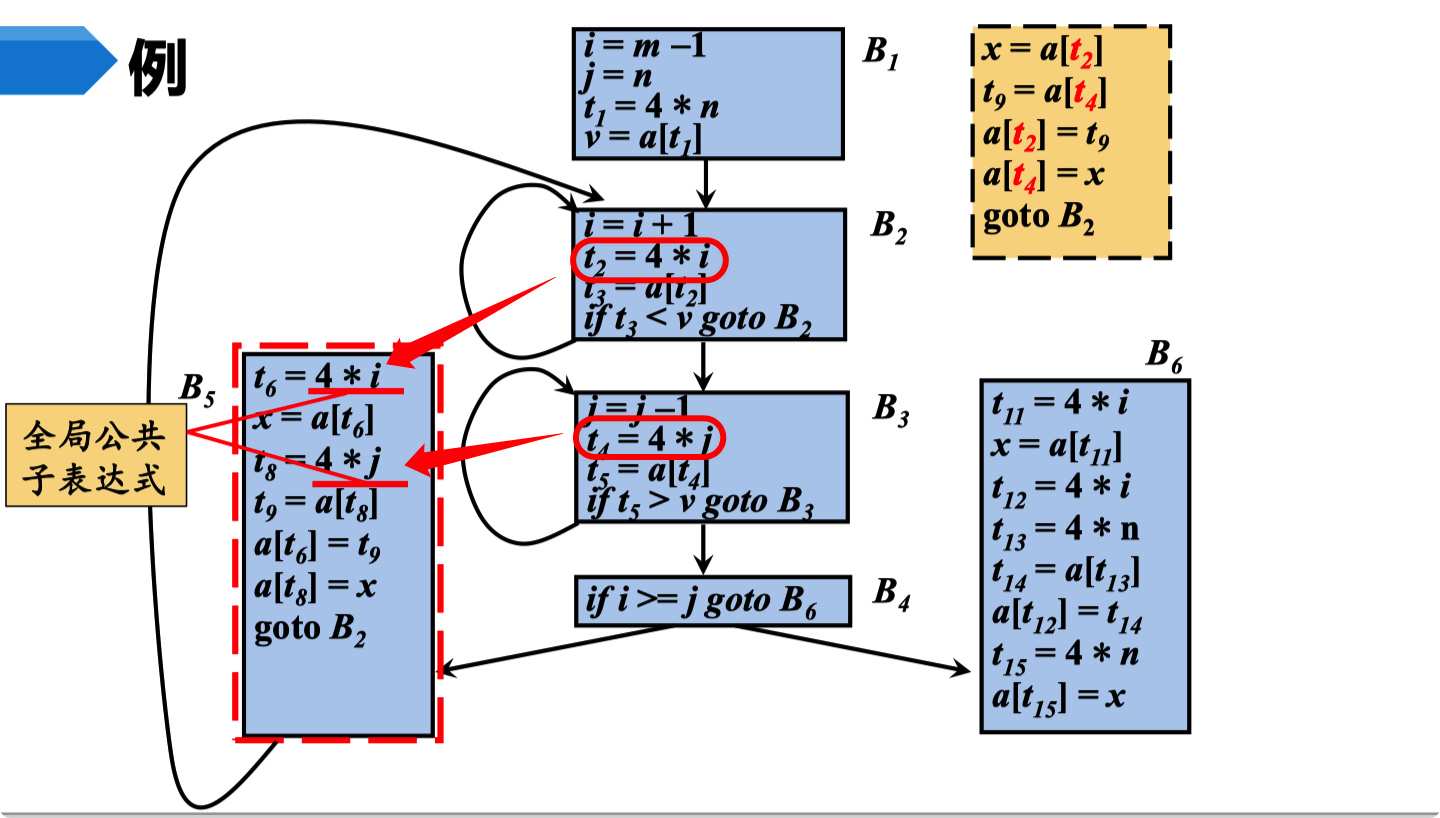
image-20200717194424843

删除公共表达式

我们就是要 从 局部->全局 依次删除。达到简化的目的。

删除无用代码

复制传播

  1. 常用的公共子表达式消除算法和其它一些优化算法会引入 一些复制语句 (形如x = y的赋值语句)
  2. 复制传播：在复制语句x = y之后尽可能地用y代替x。 （复制传播给删除无用代码带来机会）
image-20200717200547372

​ 无用代码(死代码Dead-Code ) ： 其计算结果永远不会被使用的语句

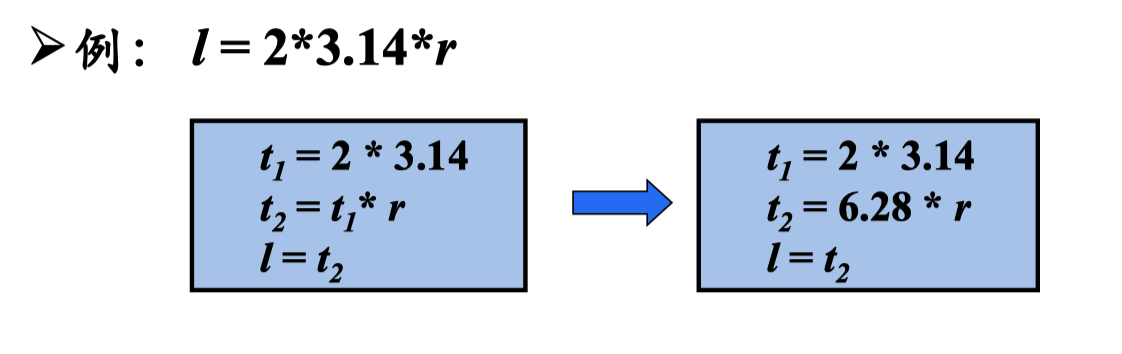
常量合并

如果在编译时刻推导出一个表达式的值是常量，就可以 使用该常量来替代这个表达式。该技术被称为常量合并

image-20200717201443004

代码移动

这个转换处理的是那些不管循环执行多少次都得到相同

结果的表达式(即循环不变计算，loop-invariant computation) ， 在进入循环之前就对它们求值

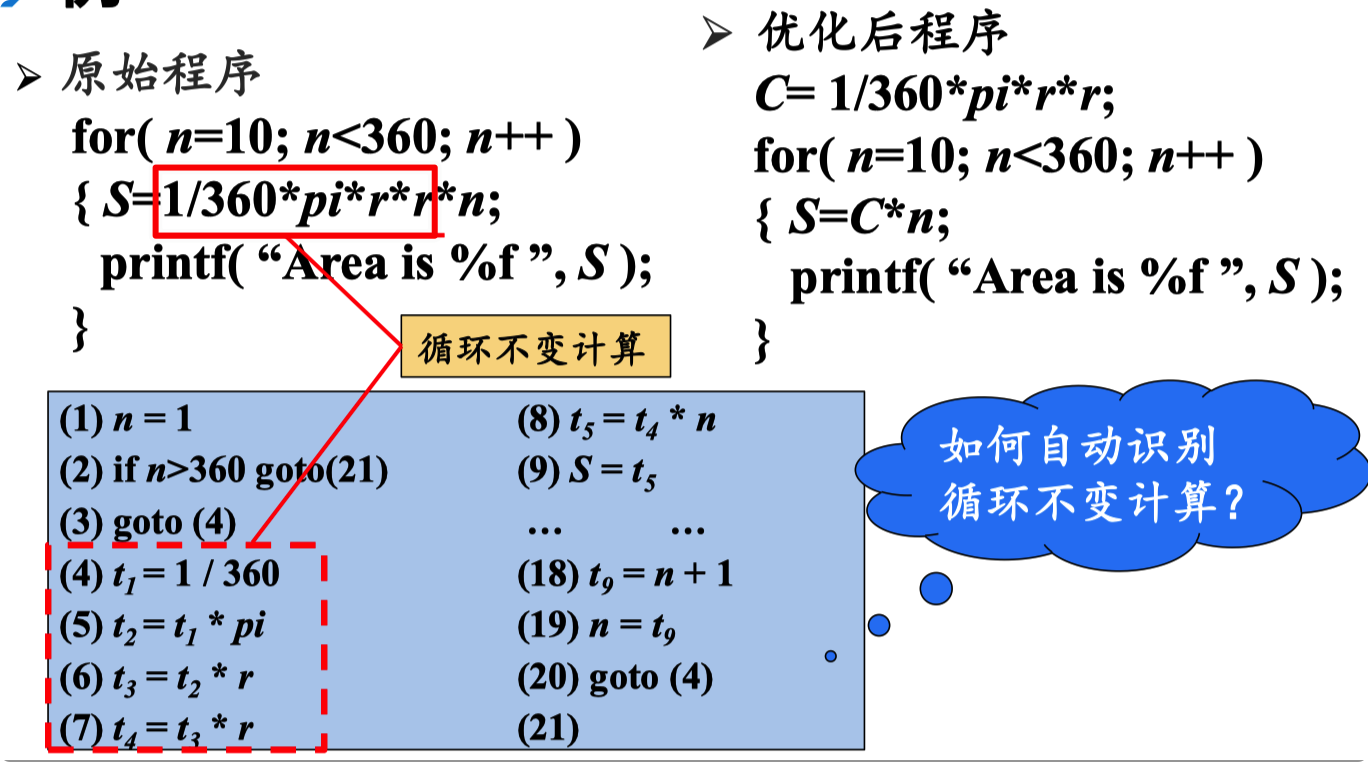
image-20200717201949998

循环不变就有一定的相对性

强度削弱

用较快的操作代替较慢的操作，如用加代替乘

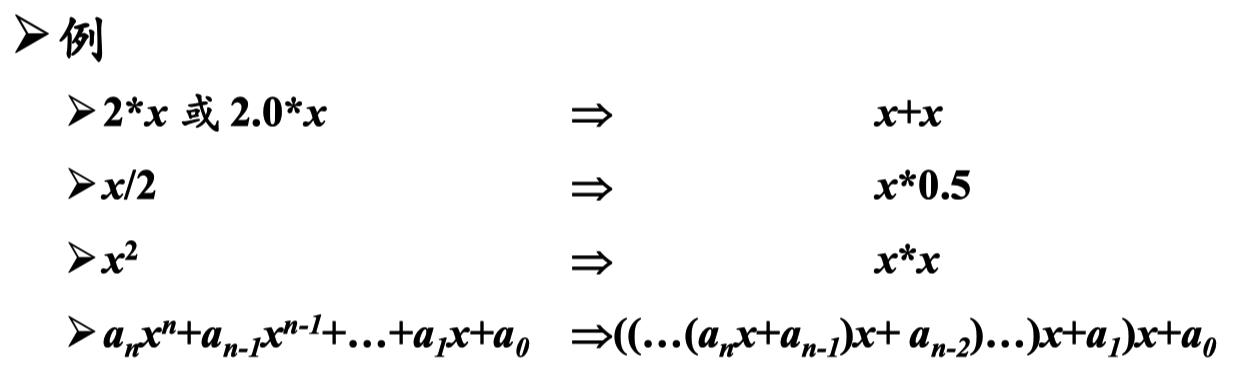
image-20200717202411473

归纳变量

对于一个变量x ，如果存在一个正的或负的常数c使

得每次x被赋值时它的值总增加c ，那么x就称为归纳 变量(Induction Variable)

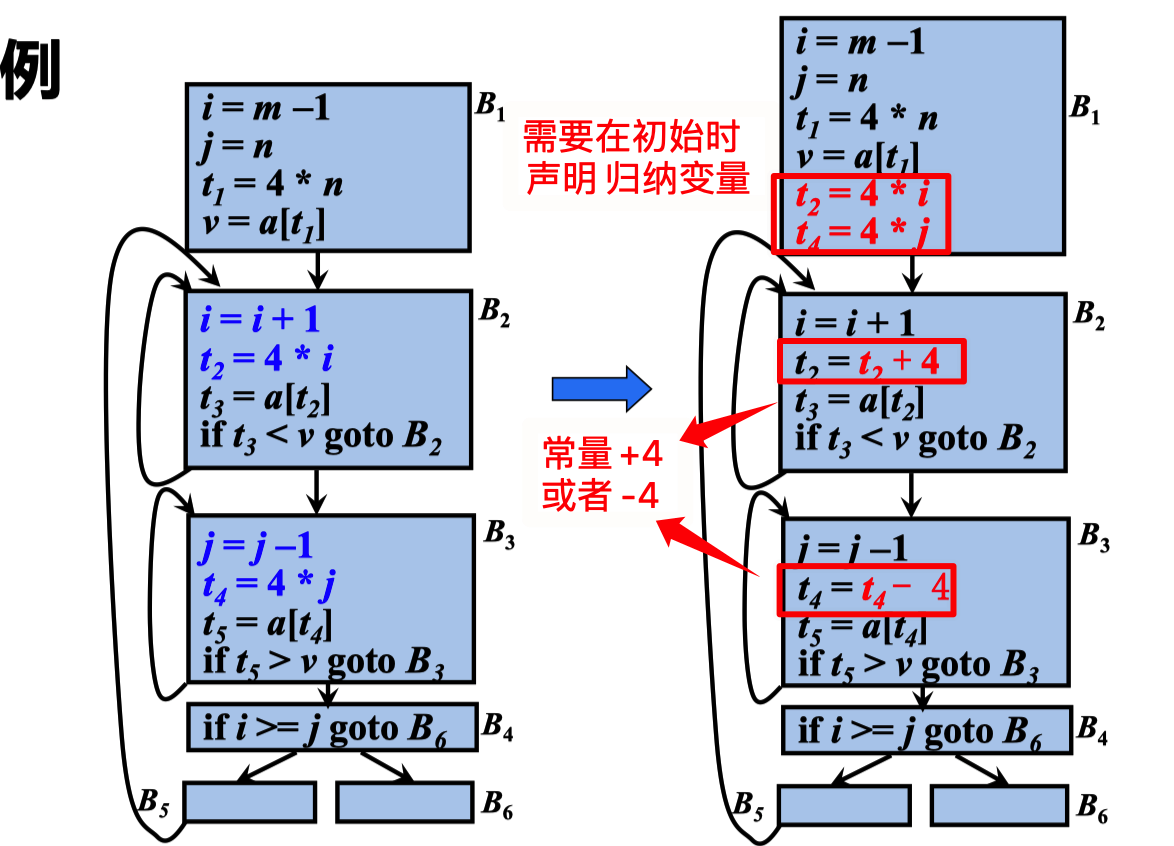
​ image-20200717203200807

删除归纳变量

在沿着循环运行时，如果有 一组归纳变量的值的变化保 持步调一致，常常可以将这 组变量删除为只剩一个

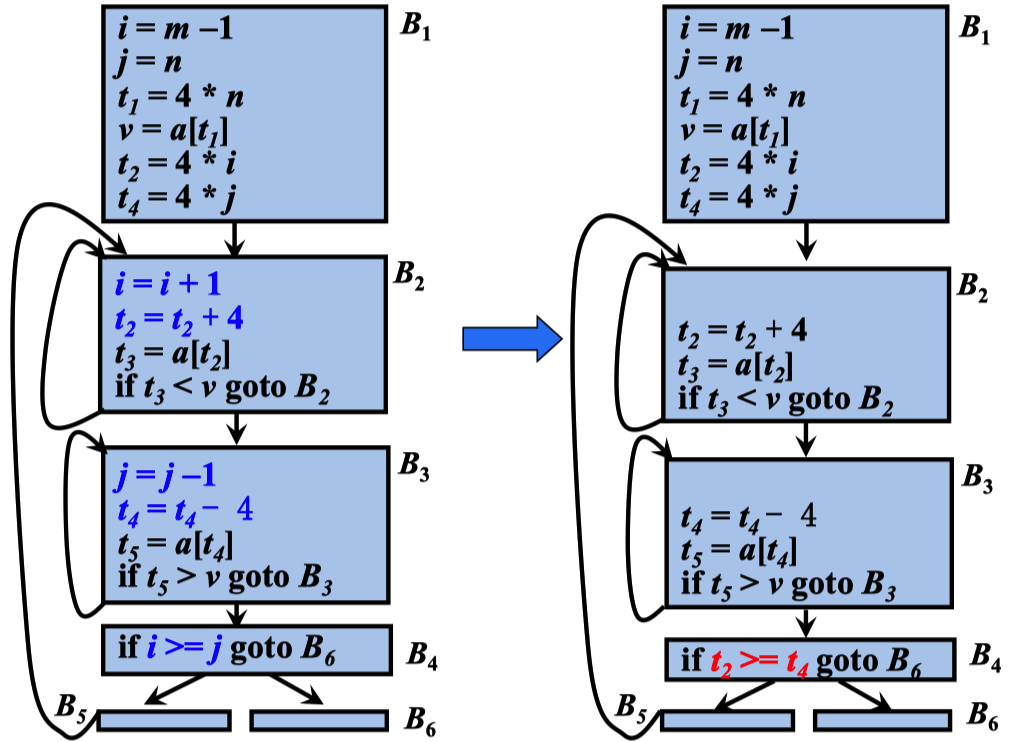
image-20200717204227826

其中 i 和 t2 ，j 和 t4 的变化是步调一致的 t2=4 * (i+1); t4=4 * (j-1) 最后又有一个 if 的比较跳转。
也是比较的 i和j 这个时候我们就可以 将 i>=j 转化为 t2>=t4

基本块的优化

很多重要的局部优化技术首先把一个基本块转换成为

一个无环有向图(directed acyclic graph，DAG)

  1. 检测公共表达式。
  2. 删除无用代码。

基本块的 DAG

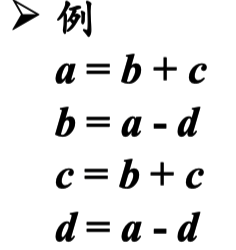
image-20200717221653556

基本块中的每个 语句s 都对应一个 内部结点 N

  1. 结点N的标号是s中的 运算符；同时还有一个定值变量表被关联到N ，表示s是 在此基本块内最晚对表中变量进行定值的语句
  2. N的子结点是基本块中在s之前、最后一个对s所使用的 运算分量 进行定值的语 句对应的结点。如果s的某个运算分量在基本块内没有在s之前被定值，则这 个运算分量对应的子结点就是代表该运算分量初始值的叶结点(为区别起见， 叶节点的定值变量表中的变量加上下脚标0)
  3. 在为语句x=y+z构造结点N的时候，如果x已经在某结点M的定值变量表中，则 从M的定值变量表中删除变量x

作图为

对于形如x=y+z的三地址指令， 如果已经有一个结点表示y+z， 就不往DAG中增加新的结点， 而是给已经存在的结点附加 定值变量x。注意，如第一 第三，语句，以为在 第三之前 第二句 对第三句用到的 b 进行了一个运行，所以b+c不是公共表达式，要分开写。

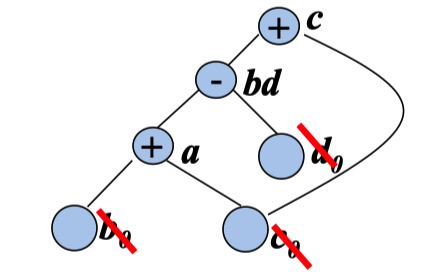
image-20200717222029221

基于 DAG 删除无用变量

通过根节点 删除无用变量。（是否为活跃变量，指在之后的运算中没有用到的变量）

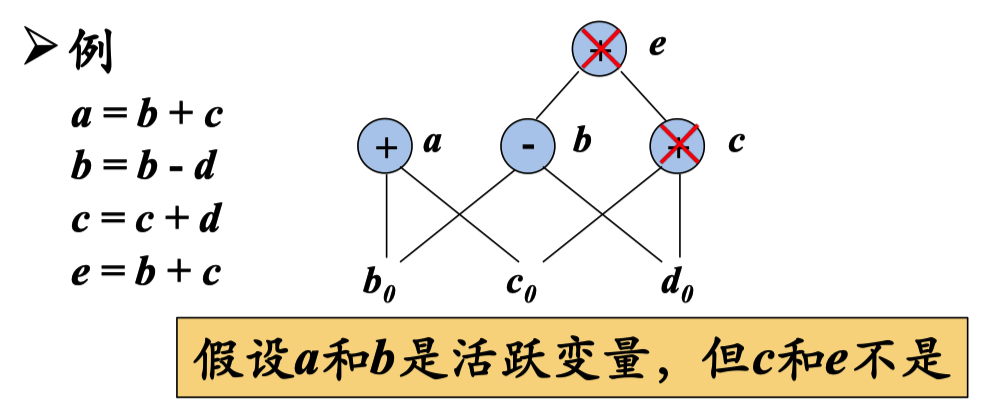
image-20200717223018649

因为 c 和 e 不是活跃变量，所以直接删除。

数组元素赋值指令的表示

用于判断 是否能成为 公共子表达式

  1. 对于形如a[j] = y的三地址指令， 创建一个运算符为“[]=”的结 点，这个结点有3个子结点， 分别表示a、j和y
  2. 该结点没有定值变量表
  3. 该结点的创建将杀死所有已经 建立的、其值依赖于a的结点
  4. 一个被杀死的结点不能再获得 任何定值变量，也就是说，它 不可能成为一个公共子表达式

image-20200717224330188

对于这个 赋值，我们的 i 和 j 可能会是 同一个值 就说嘛 z=a[i] 赋值的时候 可能 a[i] 已经被修改过了。

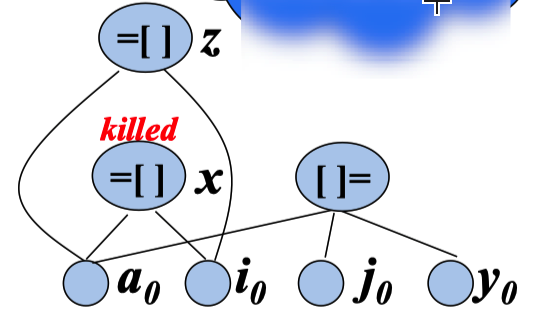
image-20200717224542087

这里 我们的 的 a0 被 []= 依赖了，所以我们遇到 杀死 x=a[i] ，重新生成 z=a[i] 也说明了 a[i] 不能作为 公共子表达式

根据基本块的DAG可以获得一些非常有用的信息

  1. 确定哪些变量的值在该基本块中赋值前被引用过（在DAG中创建了叶结点的那些变量）
  2. 确定哪些语句计算的值可以在基本块外被引用（在DAG构造过程中为语句s（该语句为变量x定值）创建的节 点N，在DAG构造结束时x仍然是N的定值变量）

从 DAG 到基本块的重组

  1. 对每个具有若干定值变量的节点，构造一个三地址语句 来计算其中某个变量的值

    • 倾向于把计算得到的结果赋给一个在基本块出口处活跃的变量(如果没有全局活跃变量的信息作为依据，就要假设所有变 量都在基本块出口处活跃，但是不包含编译器为处理表达式 而生成的临时变量)

  2. 如果结点有多个附加的活跃变量，就必须引入复制语句， 以便给每一个变量都赋予正确的值

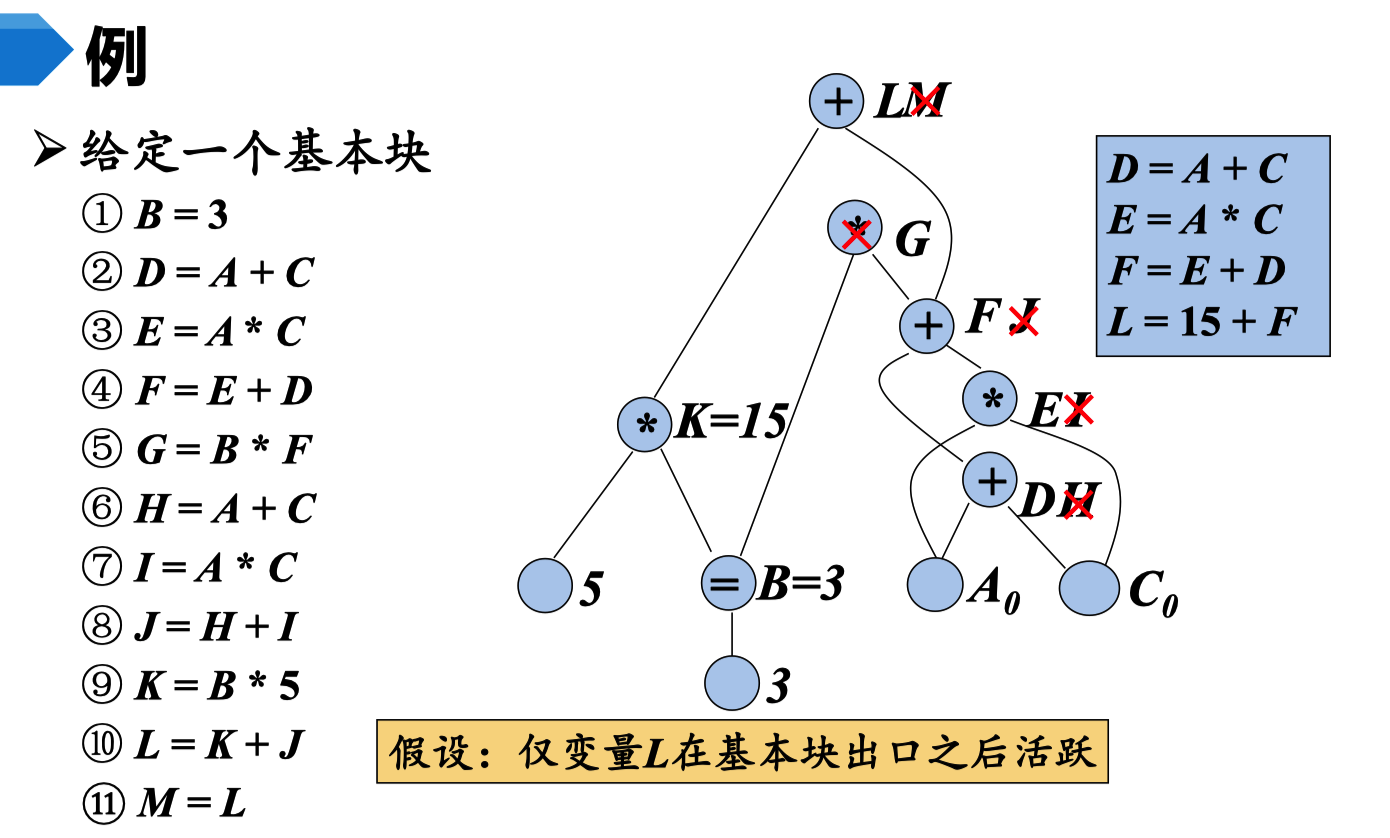
image-20200717230035215

对于 这个 DAG 表。先画出对于的 DAG （没有❌的）。这个时候我们会发现 F,J E,I D,H 都是公共子表达式。

因为 只有 L 在基本块出口之后是活跃的。所以这里面 M,G 都是没有用处的，且我们发现 B，K是一个定量。所以我们可以直接让 B，K等于他应该有的值。然后我们删除 不活跃的根节点 G,M 让删除多余的 公共子表达式。 结果为 上图带❌的。重新生成的基本快

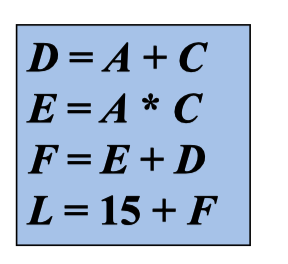
image-20200717230630119

数据流分析

一组用来获取程序执行路径上的数据流信息的技术

数据流分析应用

  1. 到达-定值分析 (Reaching-Definition Analysis)
  2. 活跃变量分析 (Live-Variable Analysis)
  3. 可用表达式分析 (Available-Expression Analysis)

在每一种数据流分析应用中，都会把每个程序点和 一个数据流值关联起来

数据流分析模式

IN[s]: 语句s之前的数据流值

OUT[s]: 语句s之后的数据流值

fs：语句s的传递函数(transfer function) (s 是 f的下标 小s)

​ 传递函数的两种风格

  1. 信息沿执行路径前向传播 (前向数据流问题)

    ​ OUT[s] = fs (IN[s])

  2. 信息沿执行路径逆向传播 (逆向数据流问题)

    ​ IN[s] = fs (OUT[s])

对于 数据流。设基本块B由语句s1, s2, … , s n顺序组成，则

​ IN[si+1 ]= OUT[si ] i=1, 2, … , n-1 i为下标

基本块上的数据流模式

和数据流模式相同，但基础从 语句 变成了 基本块。

IN[B]: 紧靠基本块B之前的数据流值

OUT[B]: 紧随基本块B之后的数据流值

设基本块B由语句s1,s2,…,s n顺序组成，则

IN[B] = IN[s1]

OUT[B] = OUT[sn]

fB：基本块B的传递函数 (B 是 f的下标 小B)

​ 前向数据流问题：OUT[B] = fB(IN[B]) f B = fsn ·…·f s2 ·fs1

​ 逆向数据流问题：IN[B] = fB(OUT[B]) f B= fs1· f s2· …·fsn

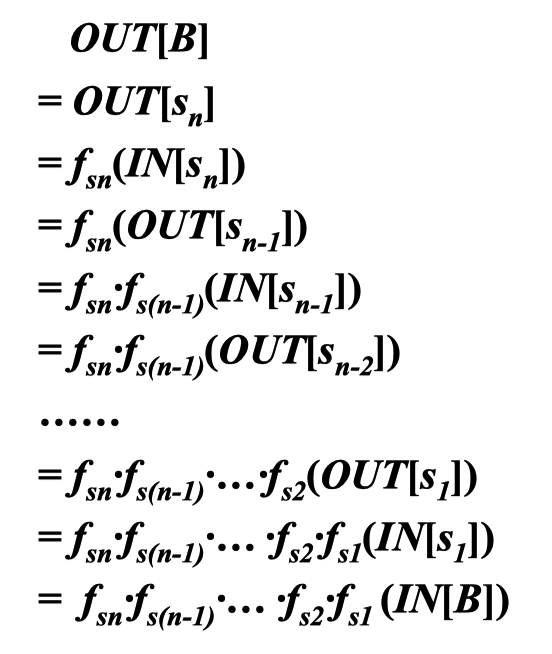
image-20200718105725863

实现依次递推 fB 是由 基本块B中的 各个语句传递函数，反向依次合成的。

到达定值分析

定值 变量x的定值是(可能)将一个值赋给x的语句

到达定值

  1. 如果存在一条从紧跟在定值d后面的点到达某一程序点p的路径， 而且在此路径上d没有被“杀死” (如果在此路径上有对变量x 的其它定值d′，则称变量x被这个定值d′“杀死”了) ，则称定 值d到达程序点p
  2. 直观地讲，如果某个变量x的一个定值d到达点p，在点p 处使用的x的值可能就是由d最后赋予的
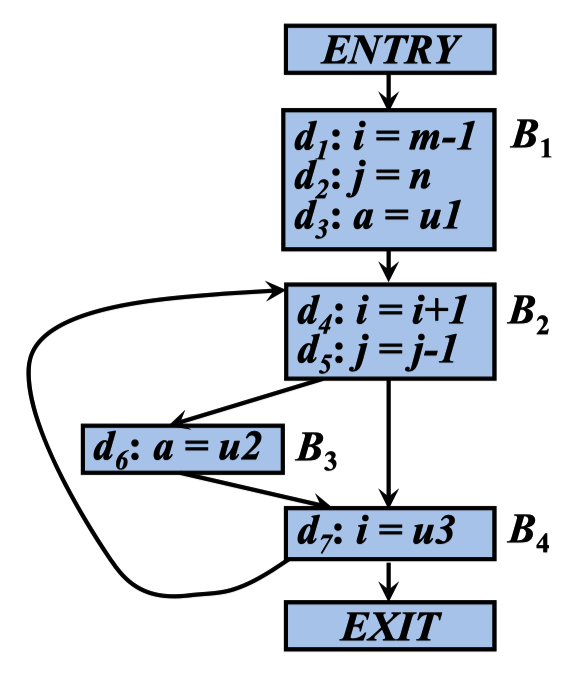
image-20200718143116380

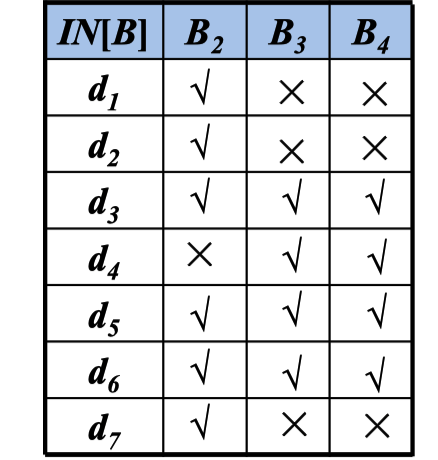
得到 B2 B3 B4 块进入的订制是多少。 不能进入，就说明这个值在进入之前，已经被重新赋值了，这个时候，这个值就被杀死了，就不能进入到对应的块。

假设每个控制流图都有两个空基本块， 分别是表示流图的开始点的ENTRY结 点和结束点的EXIT结点（所有离开该 图的控制流都流向它）

image-20200718143128616

到达定值分析的主要用途

循环不变计算的检测

如果循环中含有赋值x=y+z ，而y和z所有可能的定值都在循环 外面(包括y或z是常数的特殊情况) ，那么y+z就是循环不变计算

常量合并

如果对变量x的某次使用只有一个定值可以到达，并且该定值 把一个常量赋给x ，那么可以简单地把x替换为该常量

判定变量x在p点上是否未经定值就被引用

“生成”与“杀死”定值

定值d: u = v + w

​ 该语句“生成”了一个对变量u的定值d，并“杀死” 了程序中其它对u的定值

这个地方的 u 被重新赋值了。所以，在这之前的u的定值的都已经不存在了。

也就是被杀死了。

a: u = e + r

b: u = o + z

这个时候 变量u先生成一个定值a 。但是在这之后 变量u又被重新生成了 b 这个时候我们的定值a 就已经被杀死了

到达定值的传递函数

fd ：定值d: u = v + w的传递函数

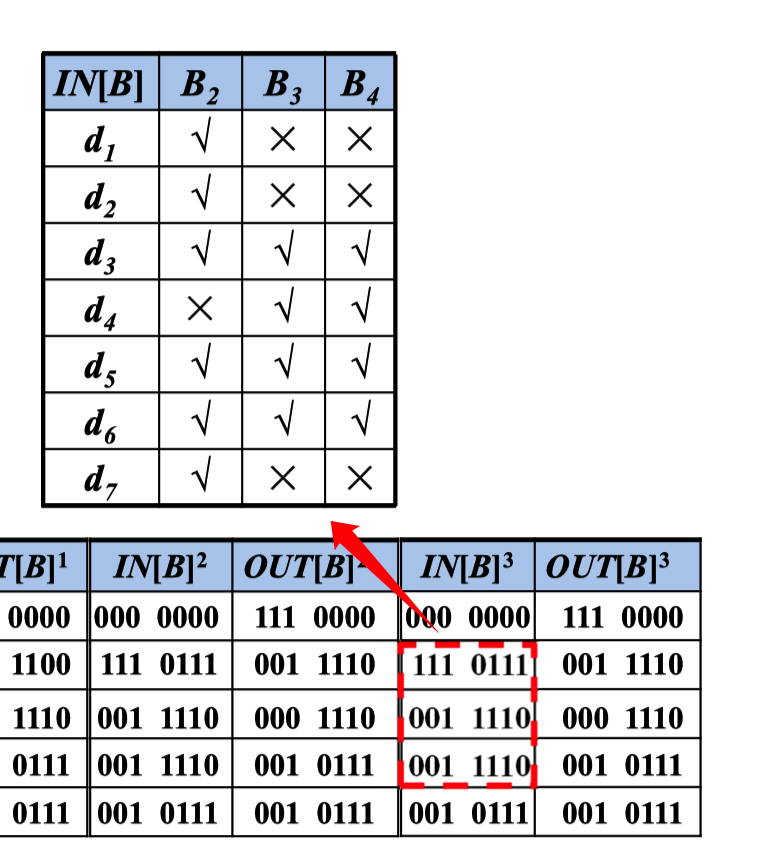
fd(x) = gend ∪(x-kill d)

生成-杀死形式

gend ： 由语句d生成的定值的集合 gend ={d}

killd ：由语句d杀死的定值的集合（程序中所有其它对u的定值）

经过每个 传递函数 时，都要杀死重新赋值的变量，然后加入数组。

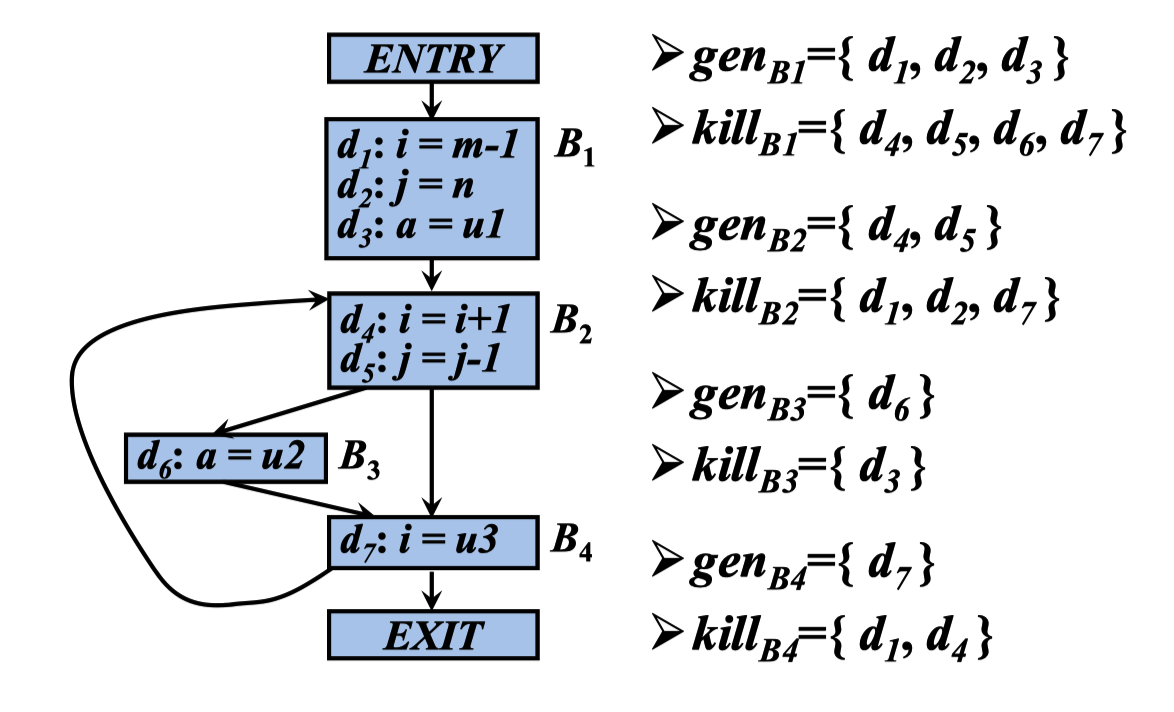
image-20200718160652273

到达定值的数据流方程

IN[B]：到达流图中基本块B的入口处的定值的集合

OUT[B] ：到达流图中基本块B的出口处的定值的集合

image-20200719221335739

到达定值方程的计算

到达定值方程的计算

输入：

​ 流图G，其中每个基本块B的gen B 和kill B 都已计算出来

输出：

​ IN[B]和OUT[B]

image-20200719222040382

例题

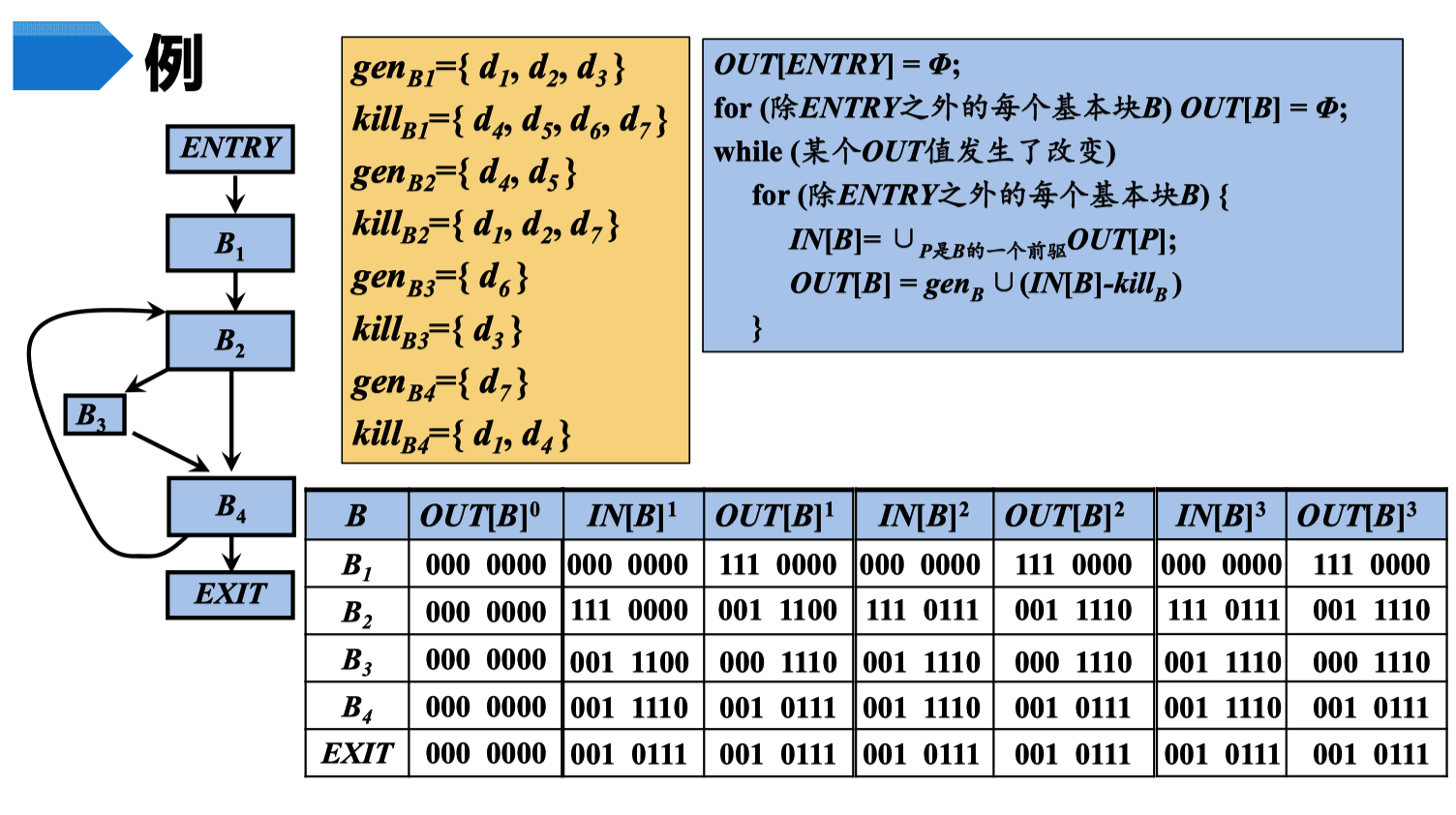
image-20200719223021831
  1. 将这个块，引入的块，的out 值取并集
image-20200719223040216
  1. 这个块的 out 值 为， 这个快接受的 IN[B] 的值 + gen对应块的值 - kill对应块的值 = OUT[B] 也就是这个块的输出
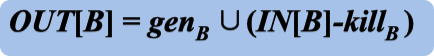
image-20200719223212141

一直重复迭代，直到 所有的 OUT[B] 的值和上一次迭代相同。(OUT3 所有的值 和 OUT2 的值对应相同)

然后更具 IN[B] 的值得到表格

image-20200719223752045

引用-定值链

引用-定值链(简称ud链) 是一个列表，对于变量的每一 次引 用，到达该引用的所有定值都在该列表中

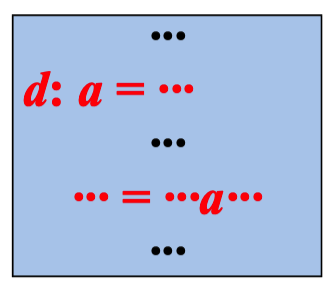
  1. 如果块B中变量a的引用之前有a的定值， d: a = ··· 那么只有a的最后一次定值会在该引用的 ··· ··· = ···a··· ud链中
image-20200719223946219

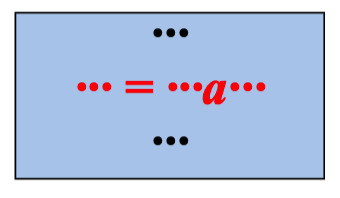
  1. 如果块B中变量a的引用之前没有a的定值， ··· ··· = ···a··· 那么a的这次引用的ud链就是IN[B]中a的 ···

    定值的集合

image-20200719224011054

活跃变量分析

活跃变量

对于变量x和程序点p，如果在流图中沿着从p开始

的某条路径会引用变量x在p点的值，则称变量x在 点p是活跃(live)的，否则称变量x在点p不活跃(dead)

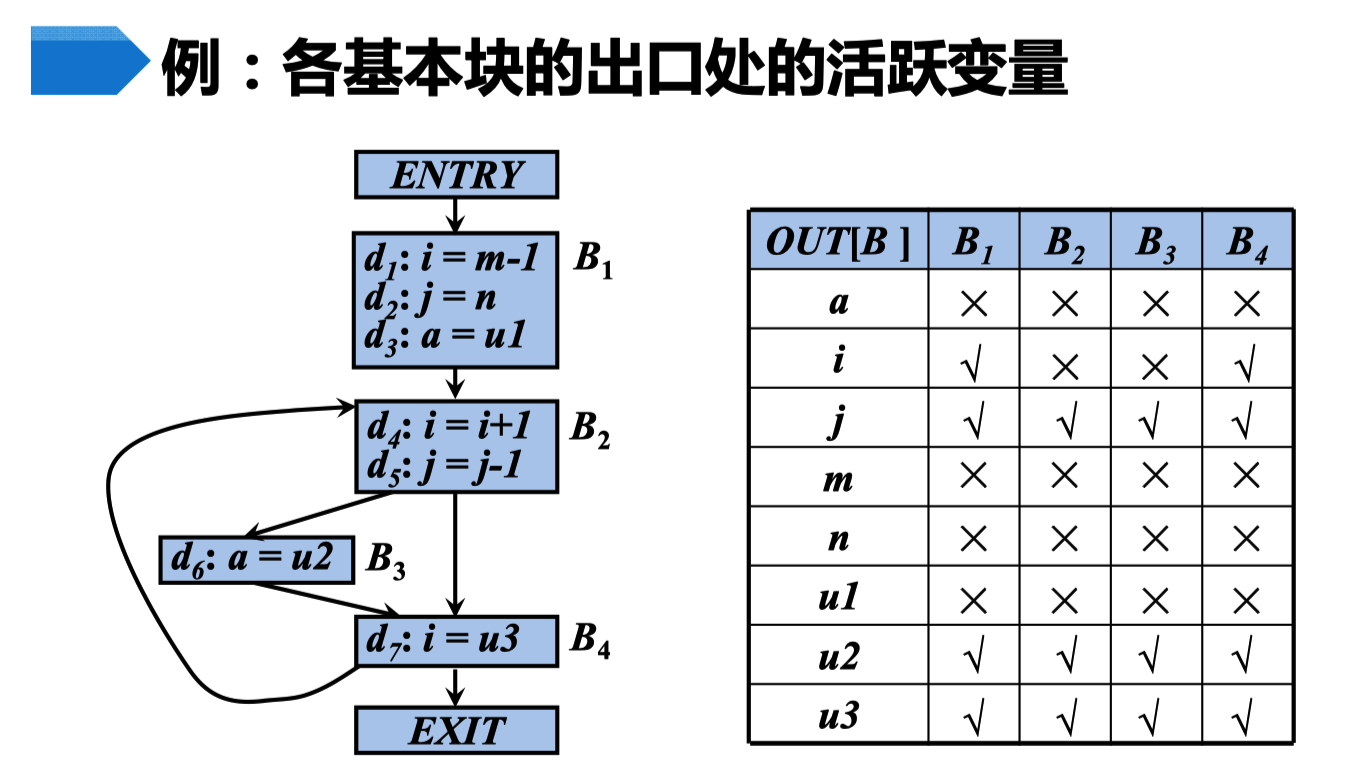
image-20200720085913028

  • 如果重新定义了，那么在重新定义被引用之前都不是活跃的。

    如：上图的 i 在 B1 出口处进入 B2 i 被引用。并且重新定值，这是B1 出口处的 i是活跃的，但是这个时候 i 被重新定值，一直到 B4 再次重新定义了 i 的值，然后 B4 进入 B2 i 被重新引用了。这个时候 B4 的 出口处的 i 就是活跃的。

  • 在各个基本块中，如果都没有再次被引用，这这个 定值就不是活跃的。

    如：上图的 m n u1

  • 控制从 基本块 B3 中离开后，都能再次回到 B3 且在流程图中 没有对 u2 重新定值。且 B3 能一直引用 u2 。所以这个 u2 在每个块出口出都是活跃的。 U3 也是如此。

活跃变量信息的主要用途

  1. 删除无用赋值

    • 无用赋值：如果x在点p的定值在基本块内所有后继点都不被引 用，且x在基本块出口之后又是不活跃的，那么x在点p的定值就 是无用的

  2. 为基本块分配寄存器

    • 如果所有寄存器都被占用，并且还需要申请一个寄存器，则应 该考虑使用已经存放了死亡值的寄存器，因为这个值不需要保 存到内存

    • 如果一个值在基本块结尾处是死的就不必在结尾处保存这个值

活跃变量的传递函数

利用 use def 来得到数据定值使用情况，逆向数据流

IN[B] = fB(OUT [B]）

f B(x) = use B∪(x-def B)

def B：在基本块B中定值，但是定值前在B中没有被 引用的变量的集合

use B ：在基本块B中引用，但是引用前在B中没有被 定值的变量集合

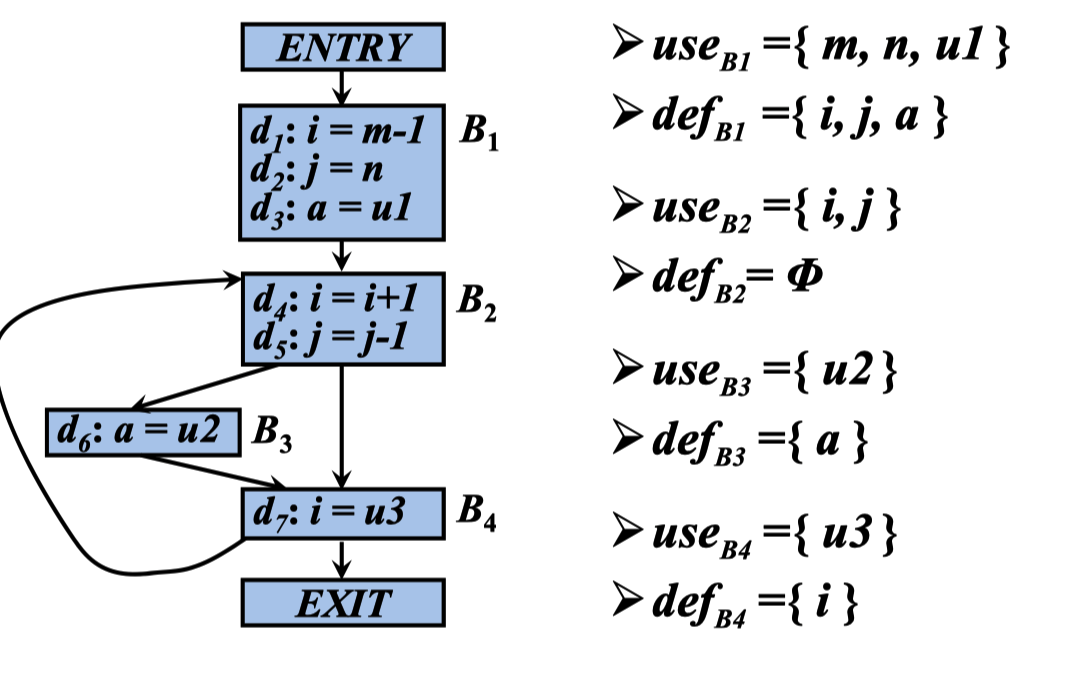
image-20200720091536672

B2 中 i 和 j 都是首次利用引用的值，所以 B2 中 use 为 i，j def 为 空

活跃变量数据流方程

IN[B]： 在基本块B的入口处的活跃变量集合

OUT[B]：在基本块B的出口处的活跃变量集合

image-20200720091916083

useB 和defB 的值可以直接从流图计算出来， 因此在方程中作为已知量

计算活跃变量的迭代算法

image-20200720091959949

例题

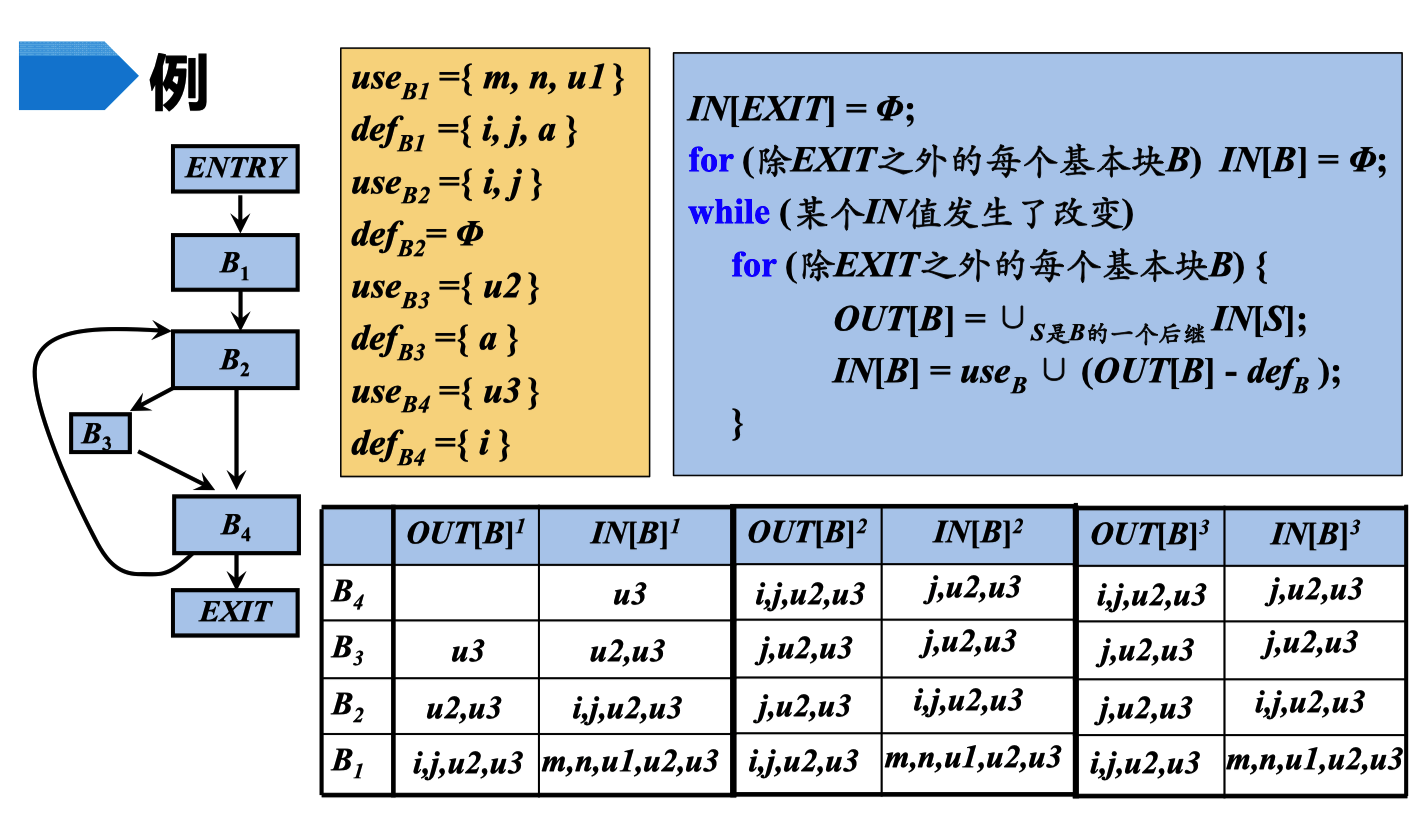
image-20200720092310385

  • 逆向推到，所以先分析 B4，B4的 IN值为。初始 + Use - def = IN[B] B4->B3->B2->B1

  • 因为B3 的值传给了 B2 所以，B3 的 OUT[B3] = IN[B4]

  • 如果 基本块的 IN 值相对上一次的 IN 值被改变了，则继续迭代

定值-引用链

定值-引用链：设变量x有一个定值d，该定值所有能够到达的引 用u的集合称为x在d处的定值-引用链，简称du链

如果在求解活跃变量数据流方程中的OUT[B]时，将OUT[B]表示 成从B的末尾处能够到达的引用的集合，那么，可以直接利用这 些信息计算基本块B中每个变量x在其定值处的du链

  1. 如果B中x的定值d之后有x的第一个定值d′， ··· d: x = ··· 则d和d′之间x的所有引用构成d的du链
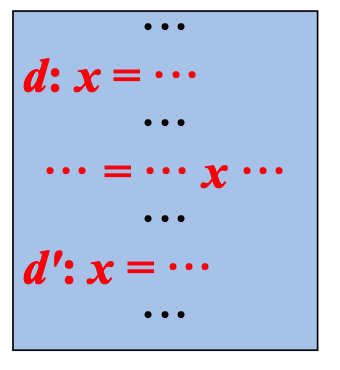
image-20200720093026399
  1. 如果B中x的定值d之后没有x的新的定值，则B中d之后x的所有引用以及OUT[B]中x的所有引用构成d的du链
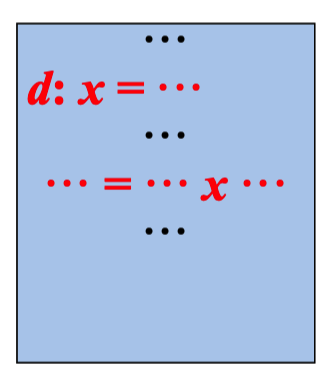
image-20200720093057828

可用表达式分析

如果从流图的首节点到达程序点 p的每条路径都对表达式x op y进行计算，并且从最后一个这样的计算到点p之 间没有再次对x或y定值，那么表达式x op y在点 p是可用 的(available)

在点 p上，x op y已经在之前被计算过，不需要重新计算 (可以直接引用。)

可用表达式信息的主要用途

  1. 消除全局公共子表达式
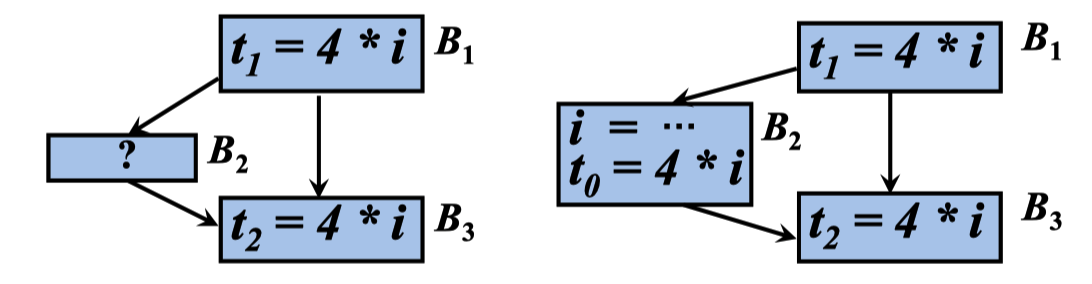
image-20200720093348137

​ 满足要求：2 中 i不能被重新定值，或者 i 被重新定值，但是出现了相同的 计算公共表达式。

  1. 进行复制传播
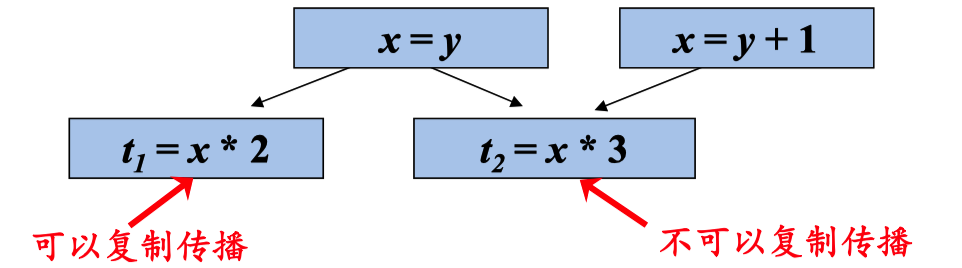
image-20200720093751897

​ 在x的引用点u可以用y代替x的条件：

​ 复制语句x = y在引用点u处可用从流图的首节点到达u的每条路径都存在复制语句x = y，并且从最后一条复 制语句x = y到点u之间没有再次对x或y定值

可用表达式的传递函数

对于可用表达式数据流模式而言，如果基本块B对x或者y进行了 (或可能进行)定值，且以后没有重新计算x op y，则称B杀死表达 式x op y。如果基本块B对x op y进行计算，并且之后没有重新定 值x或y，则称B生成表达式x op y

fB (x)= e_gen B ∪(x- e_kill B )

e_gen B ：基本块B所生成的可用表达式的集合

e_kill B ：基本块B所杀死的U中的可用表达式的集合

​ U：所有出现在程序中一个或多个语句的右部的表达式的全集

当遇到 定义 如

z=x+y 时就加入到 e_gen B

从 e_kill B中删除表达式x op y

把所有和z相关的表达式加入到 e_kill B 中

可用表达式的数据流方程

IN[B]：在B的入口处可用的U中的表达式集合

OUT[B]：在B的出口处可用的U中的表达式集合

image-20200720103309037

e_gen B 和e_kill B 的值可以直接从流图计算出来， 因此在方程中作为已知量

image-20200720103557585

支配结点和回边

如果从流图的入口结点到结点n的每条路径都经过结点d，则称结点d支配(dominate)结点n，记为d dom n

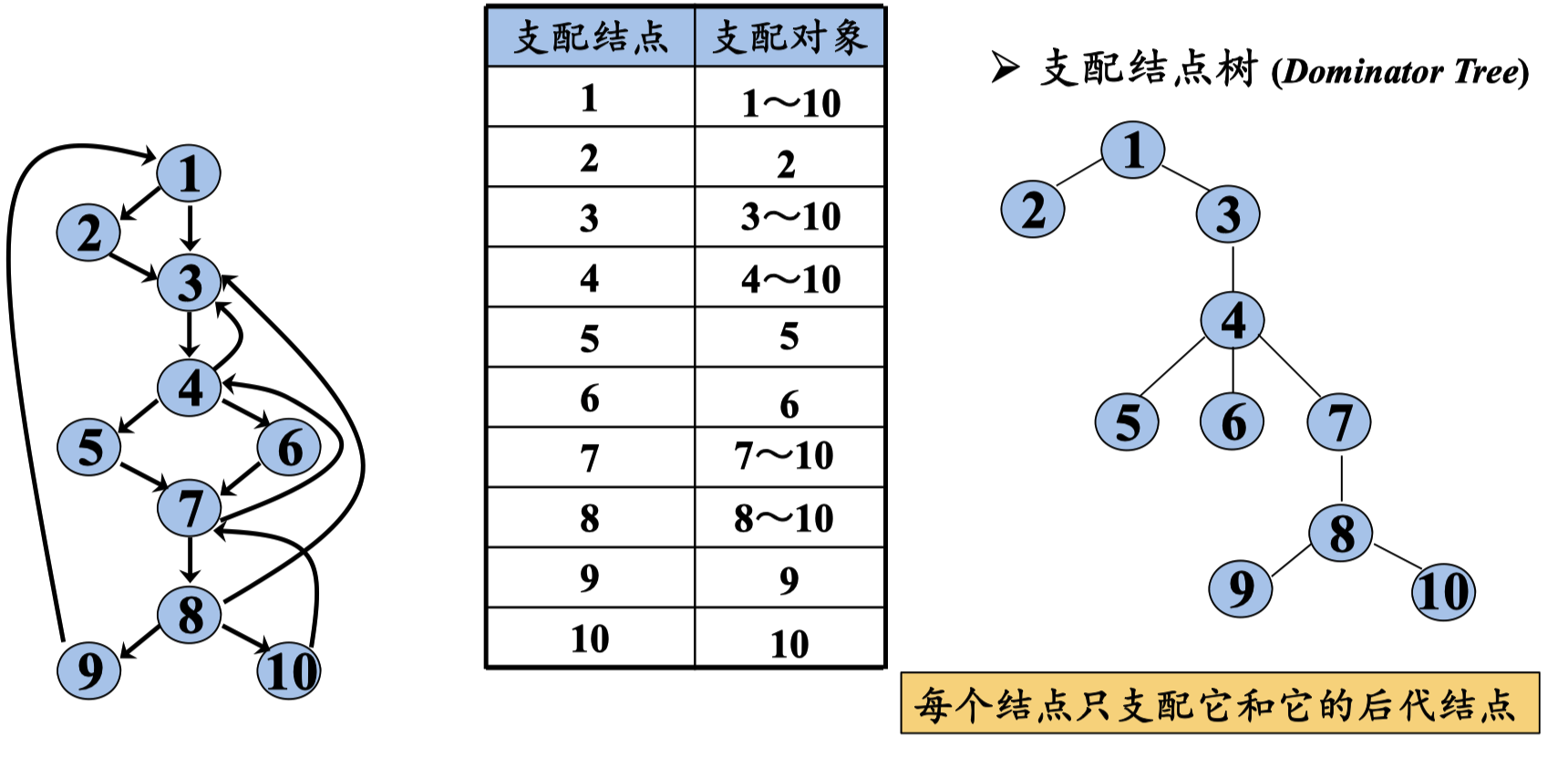
image-20200720105737586

支配对象更具到达关系确定。因为 2 ->3 也可以直接 1 -> 3 所以 2只能支配自己，5，6，9，10也是一样。

因为只支配 它 和 它的后代节点，所以 9 10只支配自己

寻找支配结点

IN[B]：在基本块B入口处的支配结点集合

OUT[B]：在基本块B出口处的支配结点集合

image-20200720110721574

计算支配结点的迭代算法

image-20200720110750417

因为什么的 是并集 ∩ 所以 初始值为 全集

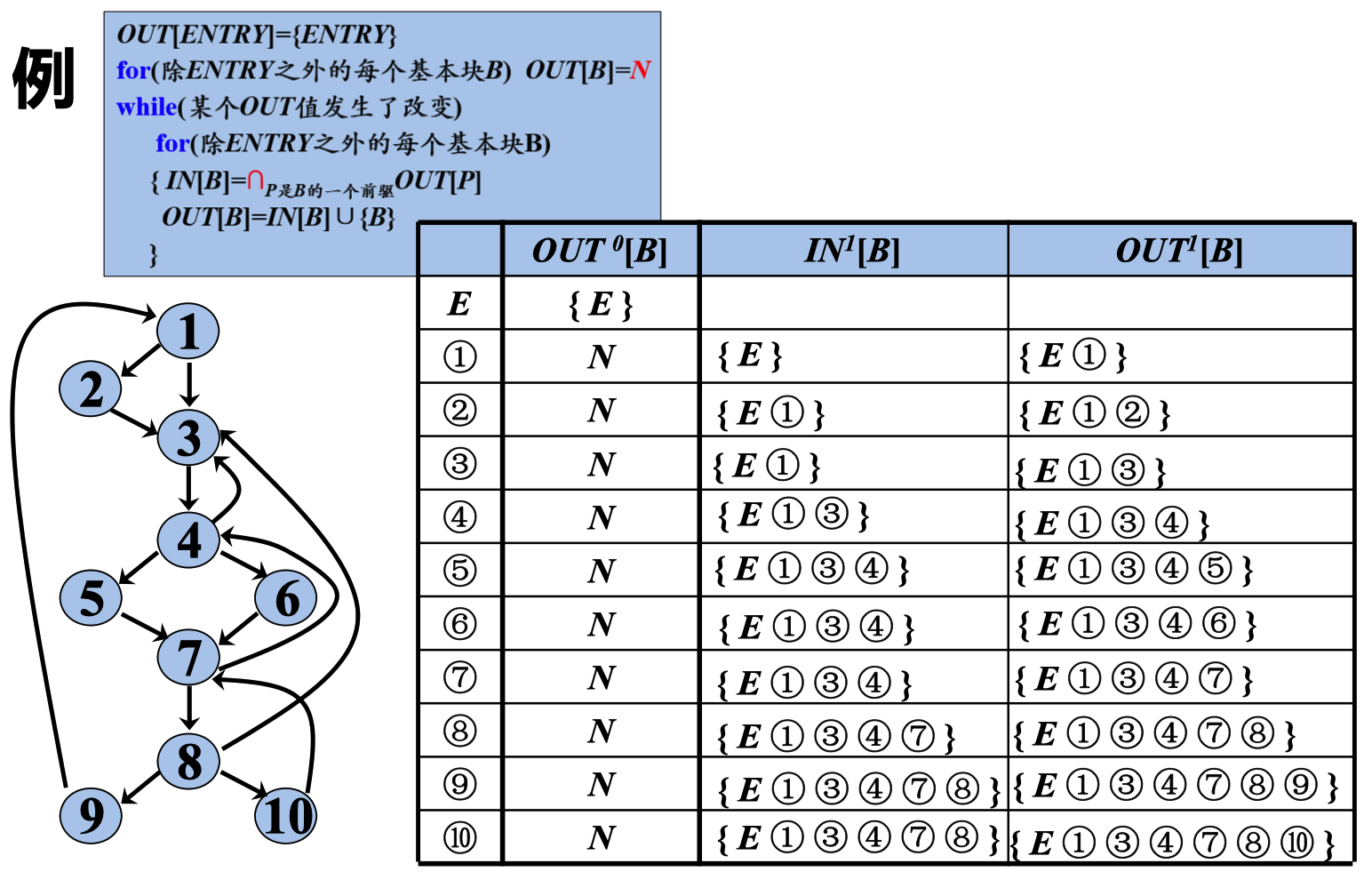
image-20200720110921360

节点 1 是 E 和 9 控制，所以 IN[B1] = E ∩ 9 =》 E , OUT[B1] 是 IN[B1] + 自身节点。

依次类推 5 号 6 号节点，都是 4号节点传入。 7号及诶按的传入， 利用的是 5 6 10 的OUT值 然后做交集。

{E①③④⑤} ∩ {E①③④⑥} ∩ N = {E①③④}

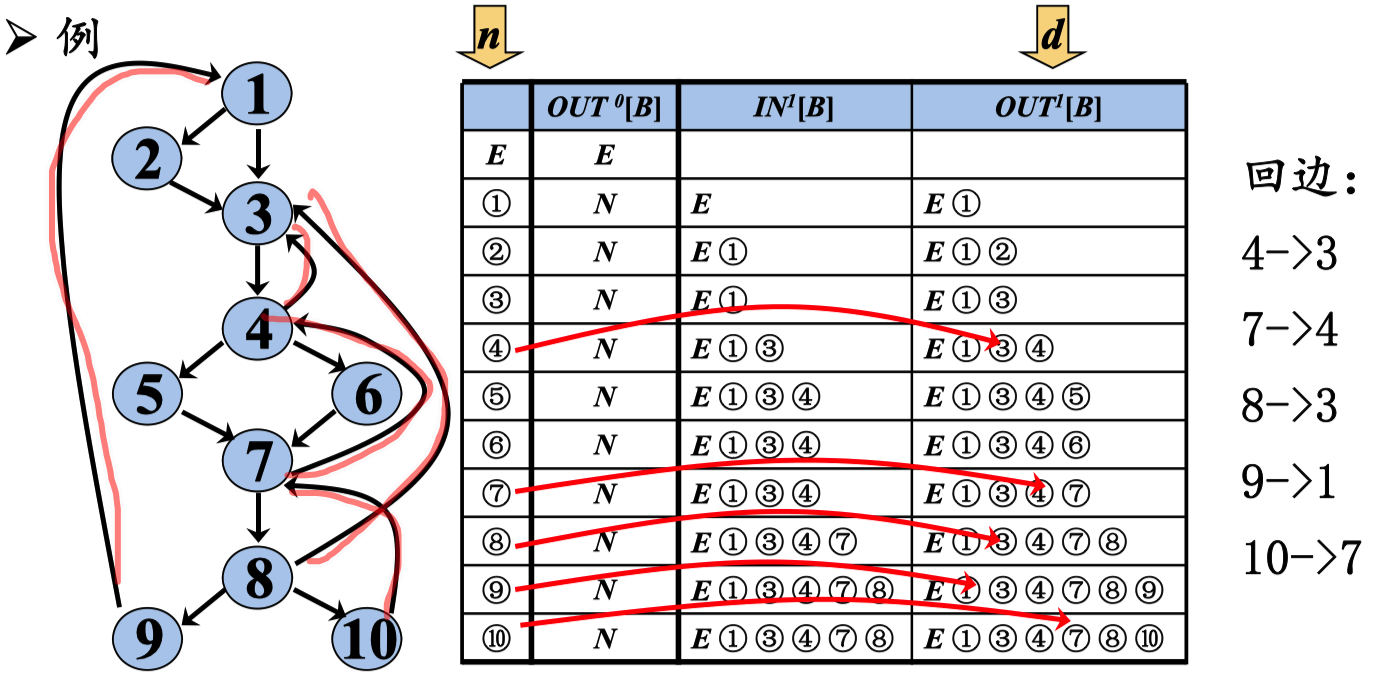
回边

假定流图中存在两个结点d和n满足d dom n。如果存在从结点 n到d的有向边n→d，那么这条边称为回边

（回到上面的节点 父辈节点）

image-20200720112005752

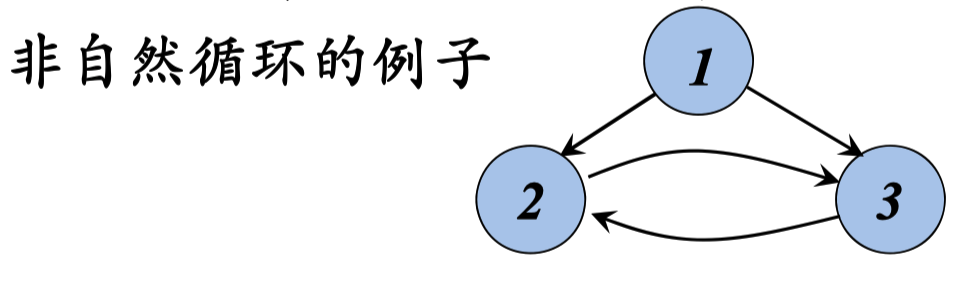
自然循环及其识别

自然循环 （自然循环是一种适合于优化的循环）

从程序分析的角度来看，循环在代码中以什么形式出 现 并不重要，重要的是它是否具有易于优化的性质

自然循环是满足以下性质的循环

  1. 有唯一的入口结点，称为首结点(header)。首结点支配循环中的 所有结点，否则，它就不会成为循环的唯一入口
  2. 循环中至少有一条返回首结点的路径，否则，控制就不可能从“循环”中直接回到循环头，也就无法构成循环
image-20200720131933941

自然循环的识别

给定一个回边n → d，该回边的自然循环为：d，以及所有可以 不经过d而到达n的结点。d为该循环的首结点。

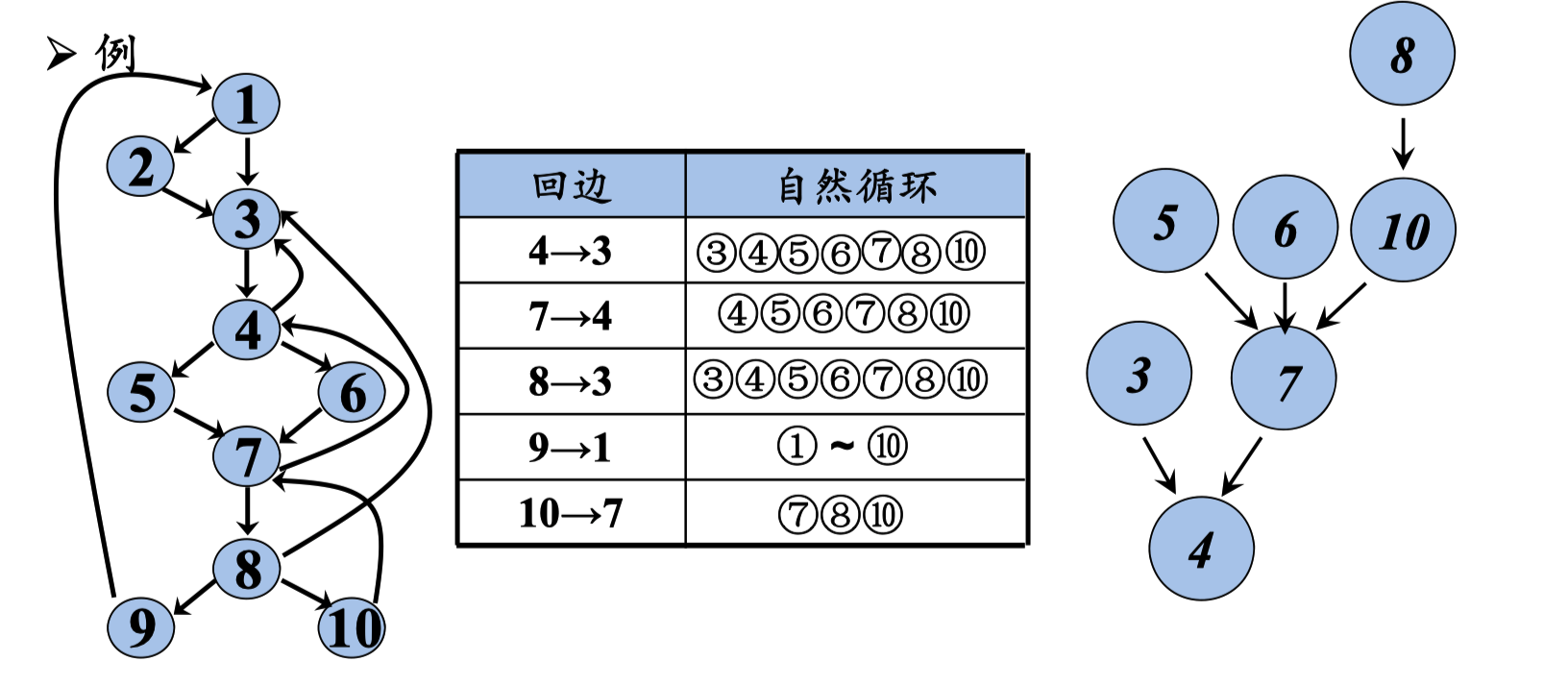
image-20200720135512654

对于第一个节点，依次向上查找。

算法：构造一条回边的自然循环

输入：流图 G和回边n → d

输出：由回边n → d的自然循环中的所有结点组成的集合

image-20200720135913364

结点d在初始时刻已经在loop中，不会去考虑它的前驱。因此, 找出的都是不 经过d而能到达n的结点。

圆环间 可以 包含。

最内循环 (Innermost Loops): 不包含其它循环的循环。

如果两个循环具有相同的首结点，那么很难说哪个是 最内循环。此时把两个循环合并

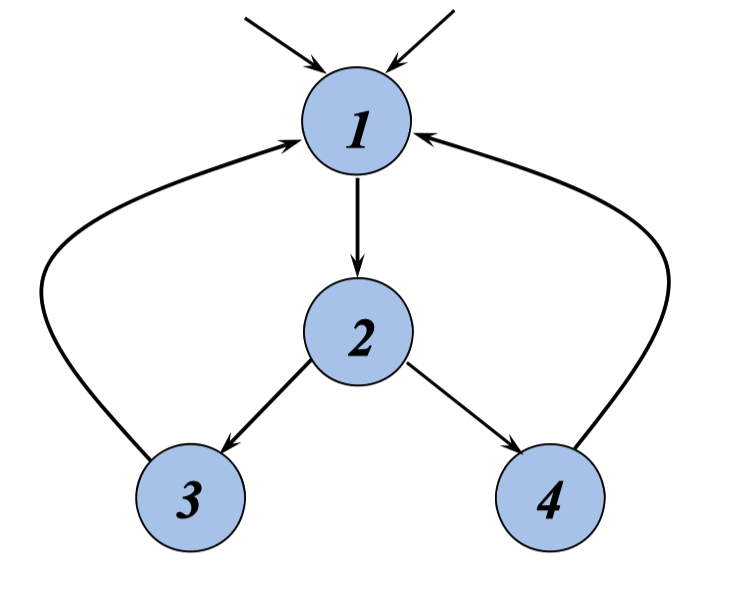
image-20200720140759959

删除全局公共子表达式 和复制语句

删除全局公共子表达式

可用表达式 的数据流问题可以帮助确定位于流图中p点的 表达式是否为 全局公共子表达式

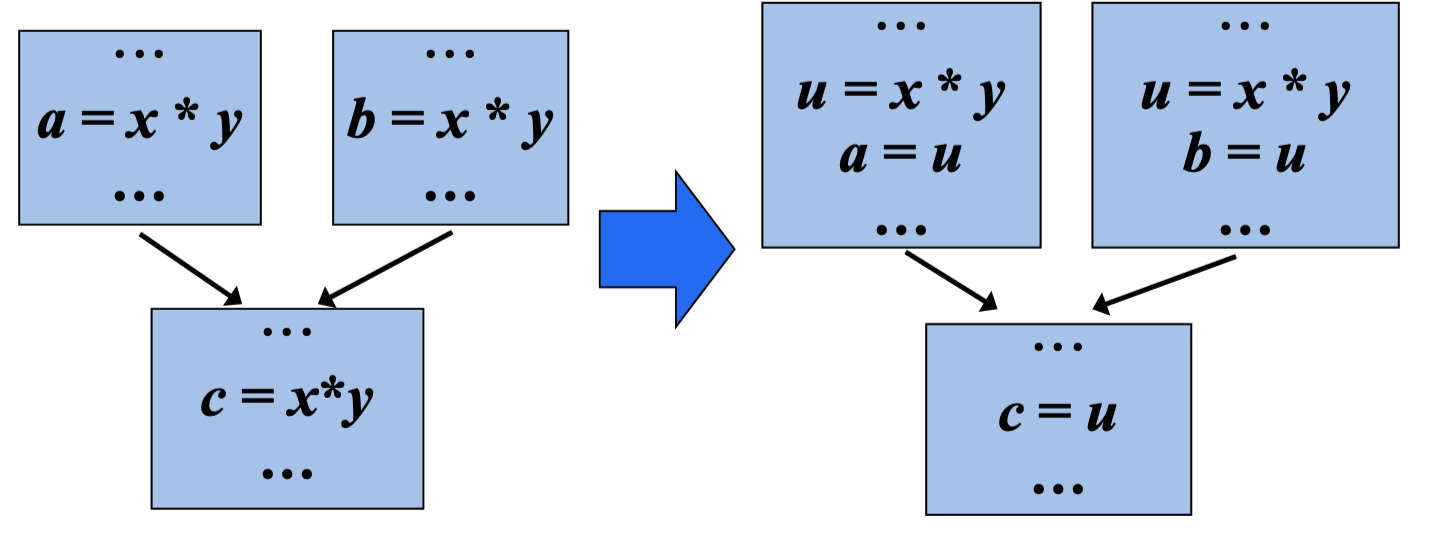
image-20200720141403910

全局公共子表达式删除算法

输入：带有可用表达式信息的流图

输出：修正后的流图

方法：

对于语句s：z = x op y，如果x op y在s之前可用，那么执行如下步骤：

① 从s开始逆向搜索，但不穿过任何计算了x o ``y的块，找到所有离 s最近的计算了x op y`的语句

② 建立新的临时变量u

③ 把步骤①中找到的语句w = x op y用下列语句代替：

1
2
u = x op y
w=u

④ 用z = u替代s

删除复制语句

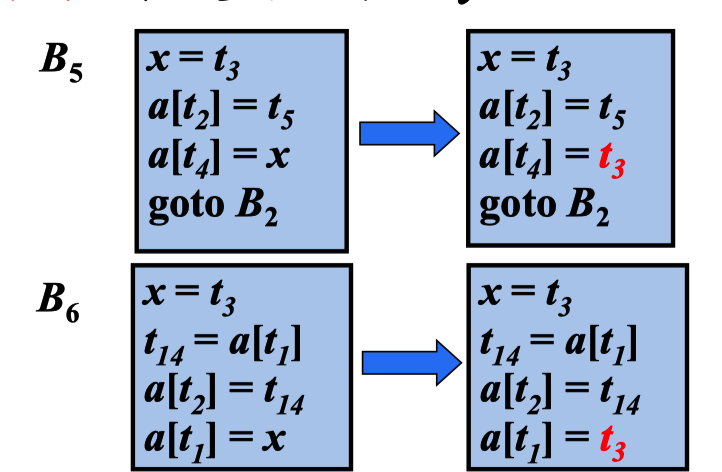
对于 复制语句 s: x=y，如果在x的所有引用点都可以用对y的 引用代替对x的引用(复制传播)，那么可以删除复制语句 x=y

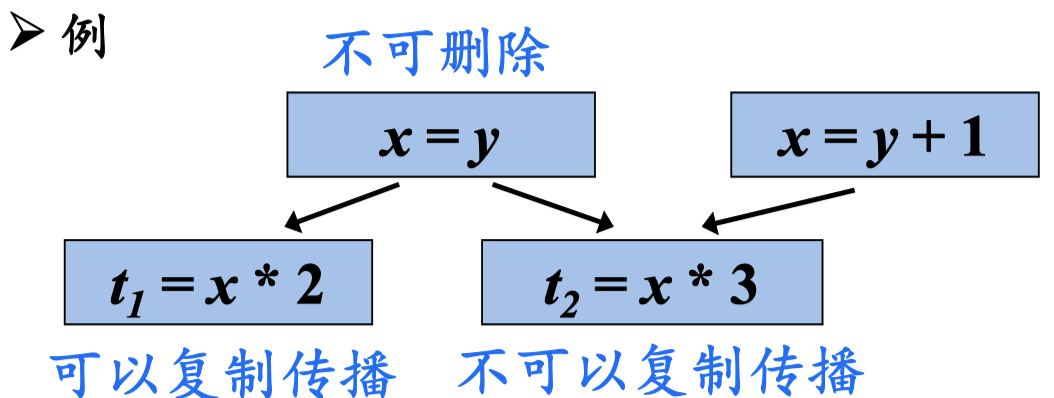
image-20200723230233823

t1 能复制传播是因为 t1 中 x的值是固定的，t2 不能复制传播，是因为 x的值可能有两种情况（x=y 或者 x=y+1）这个x的值不能被确定，所以不能利用复制传播。

※删除复制语句的算法

输入：流图G 、du链、各基本块B入口处的可用复制语句集合

输出：修改后的流图

方法：

​ 对于每个复制语句x=y，执行下列步骤

​ ① 根据du链找出该定值所能够到达的那些对x的引用

​ ② 确定是否对于每个这样的引用，x=y都在 IN[B]中(B是包 含这个引用的基本块) ，并且B中该引用的前面没有x或者y 的定值

​ ③ 如果x=y满足第②步的条件，删除x=y ，且把步骤①中找 到的对x的引用用y代替

代码移动

循环不变计算检测算法

输入：循环L，每个三地址指令的ud链

输出： L的循环不变计算语句

方法

  1. 将下面这样的语句标记为“不变”：语句的运算分量或者是常数，或者其所有定值点都在循环L外部

  2. 重复执行步骤(3)，直到某次没有新的语句可标记为“不变”为止

  3. 将下面这样的语句标记为“不变”：先前没有被标记过，且所有运 算分量或者是常数，或者其所有定值点都在循环L外部，或者只有一 个到达定值，该定值是循环中已经被标记为“不变”的语句

代码外提

循环不变计算将被移至首结点之前，为此创建一个称为 前置首结点 的新块。前置首结点 的 唯一后继是首结点 ，并且原来 从循环L外到达L首结点的边都改成进入 前置首结点。 从循环 L里面到达 首结点 的边不变

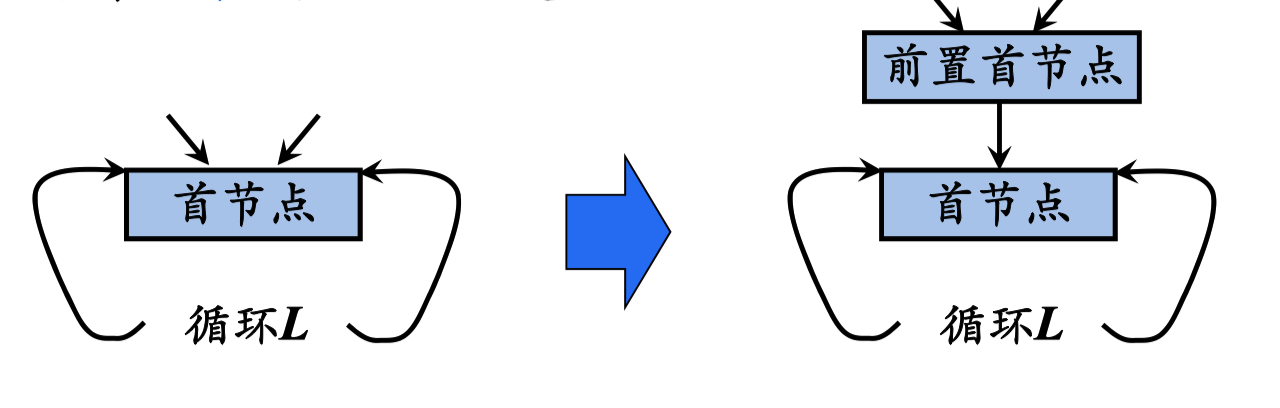
image-20200724102450237

循环不变计算语句 s : x = y + z 移动的条件

（1）s所在的基本块是循环所有出口结点(有后继结点在循 环外的结点)的支配结点

这个 语句基本块 一定会被执行。这个语句在出口节点。或者出口节点的支配节点

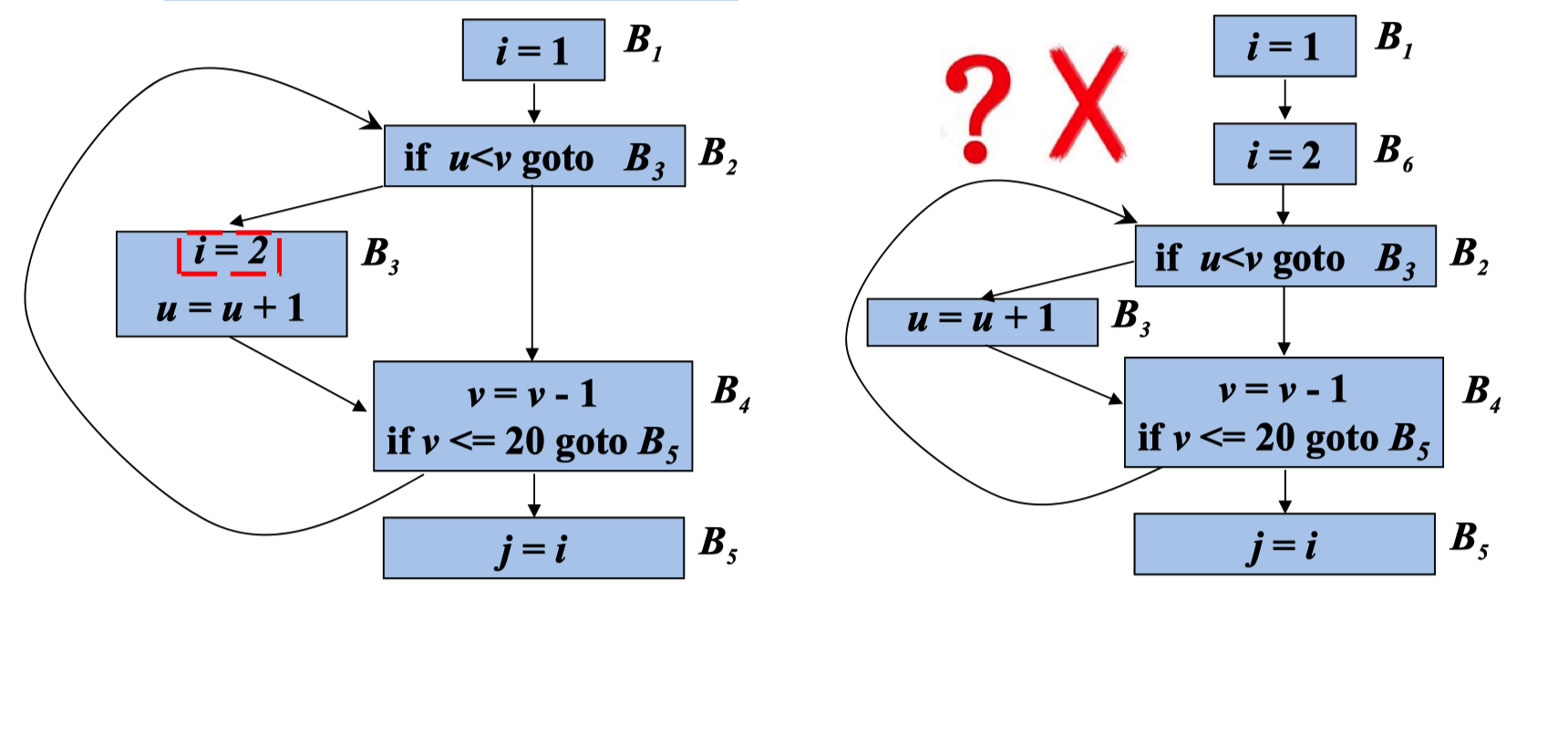
image-20200724103452709

（2） 循环中没有其它语句对x赋值

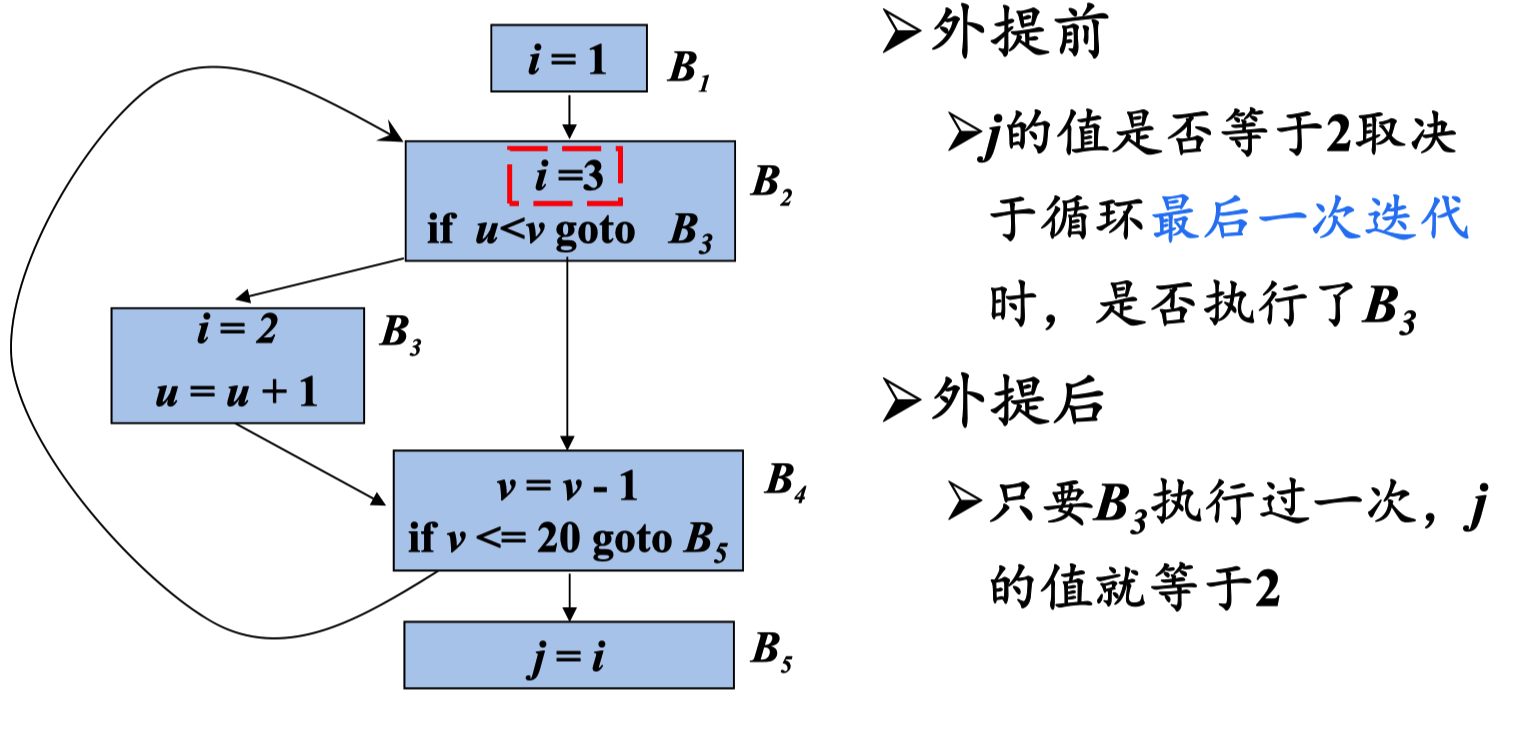
image-20200724103730978

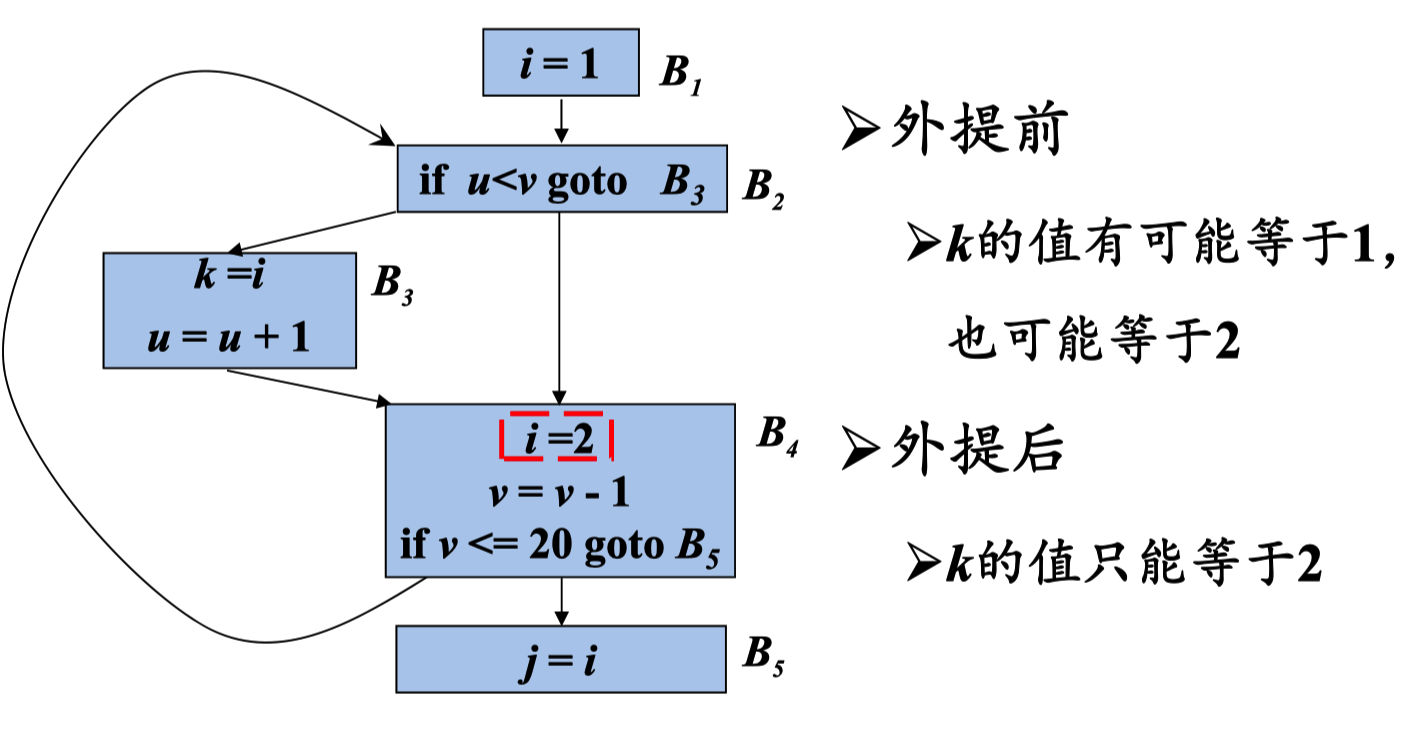
（3）循环中对x的引用仅由s到达

image-20200724104436571

代码移动算法

输入：循环L、ud链、支配结点信息

输出：修改后的循环

方法：

  1. 寻找循环不变计算
  2. 对于步骤(1)中找到的每个循环不变计算，检查是否满足上面的三个 条件
  3. 按照循环不变计算找出的次序，把所找到的满足上述条件的循环不 变计算外提到前置首结点中。如果循环不变计算有分量在循环中定 值，只有将定值点外提后，该循环不变计算才可以外提
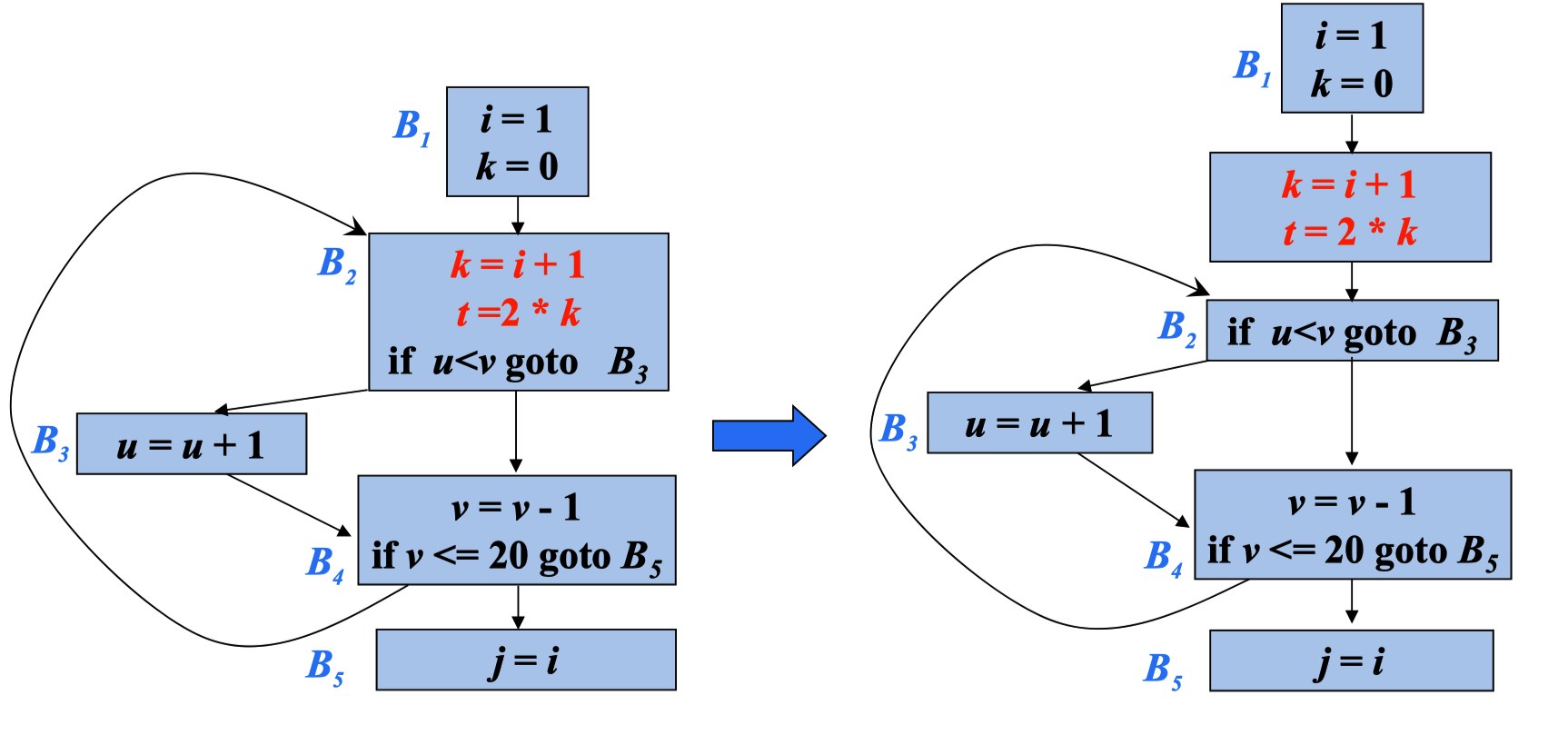
image-20200724104901600

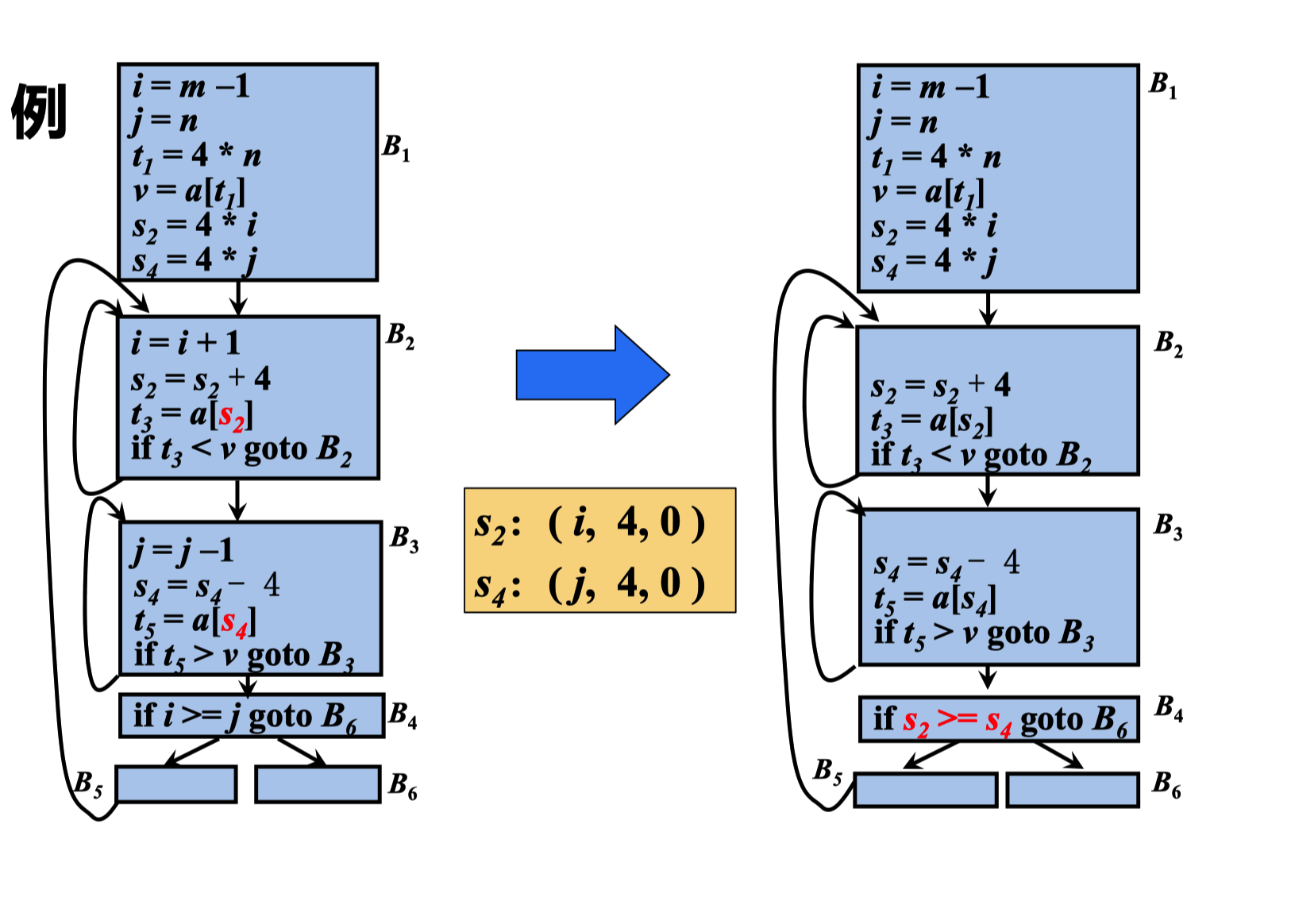
作用于归纳变量的 强度削弱

作用于归纳变量的强度削弱

  1. 对于一个变量x ，如果存在一个正的或负的常量c ，使得每次 x被赋值时，它的值总是增加c ，则称x为归纳变量

  2. 如果循环L中的变量i 只有形如i =i+c的定值(c是常量)，则称i为循环L的基本归纳变量

  3. 如果j = c×i+d，其中i是基本归纳变量，c和d是常量，则j也是一个归纳变量，称j属于i族

    ​ 基本归纳变量i属于它自己的族

  4. 每个归纳变量都关联一个三元组。如果j = c×i+d，其中i是基本归纳变量，c和d是常量，则与j相关联的三元组是( i, c, d )

图解

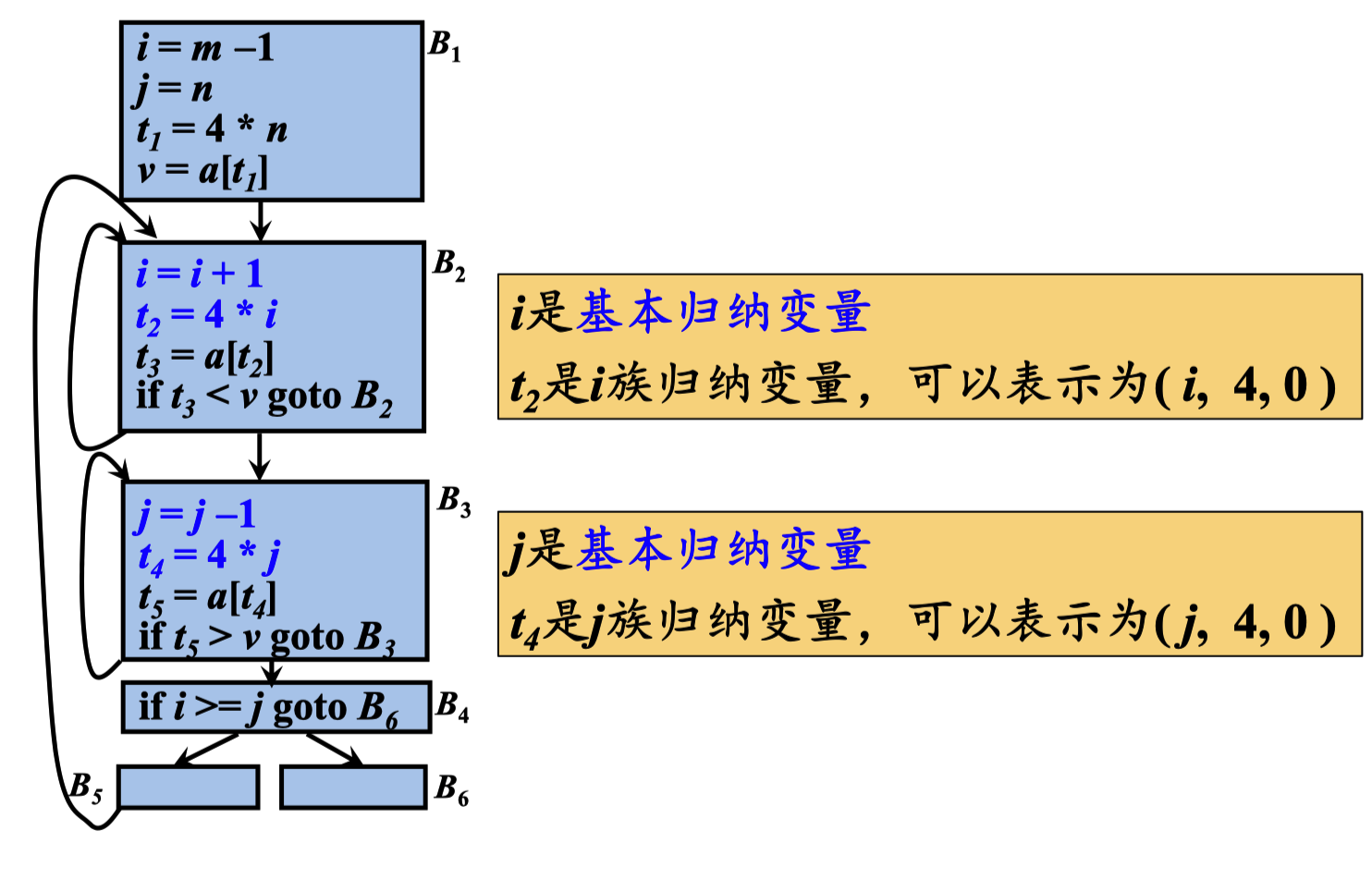
image-20200724110119485

归纳变量检测算法

输入：带有 循环不变计算信息 和 到达定值信息 的循环L

输出：一组归纳变量

​ 方法：

  1. 扫描L的语句，找出所有基本归纳变量。在此要用到 循环不变计算信息。与每个基本归纳变量i相关联的 三元组是(i, 1, 0)

作用于归纳变量的强度削弱算法

输入：带有到达定值信息和已计算出的归纳变量族的循环L

输出：修改后的循环  方法：对于每个基本归纳变量i，对其族中的每个归纳变量j：(i, c, d) 执行下列步骤

  1. 建立新的临时变量t。如果变量j1 和j2 具有相同的三元组，则只为它们建立 一个新变量

  2. 用j=t代替对j的赋值

  3. 在L中紧跟定值i=i+n之后，添加t=t+cn。将t放入i族，其三元组为 (i, c, d)

  4. 在前置节点的末尾，添加语句t=ci和t=t+d ，使得在循环开始的时候 t=c*i+d=j

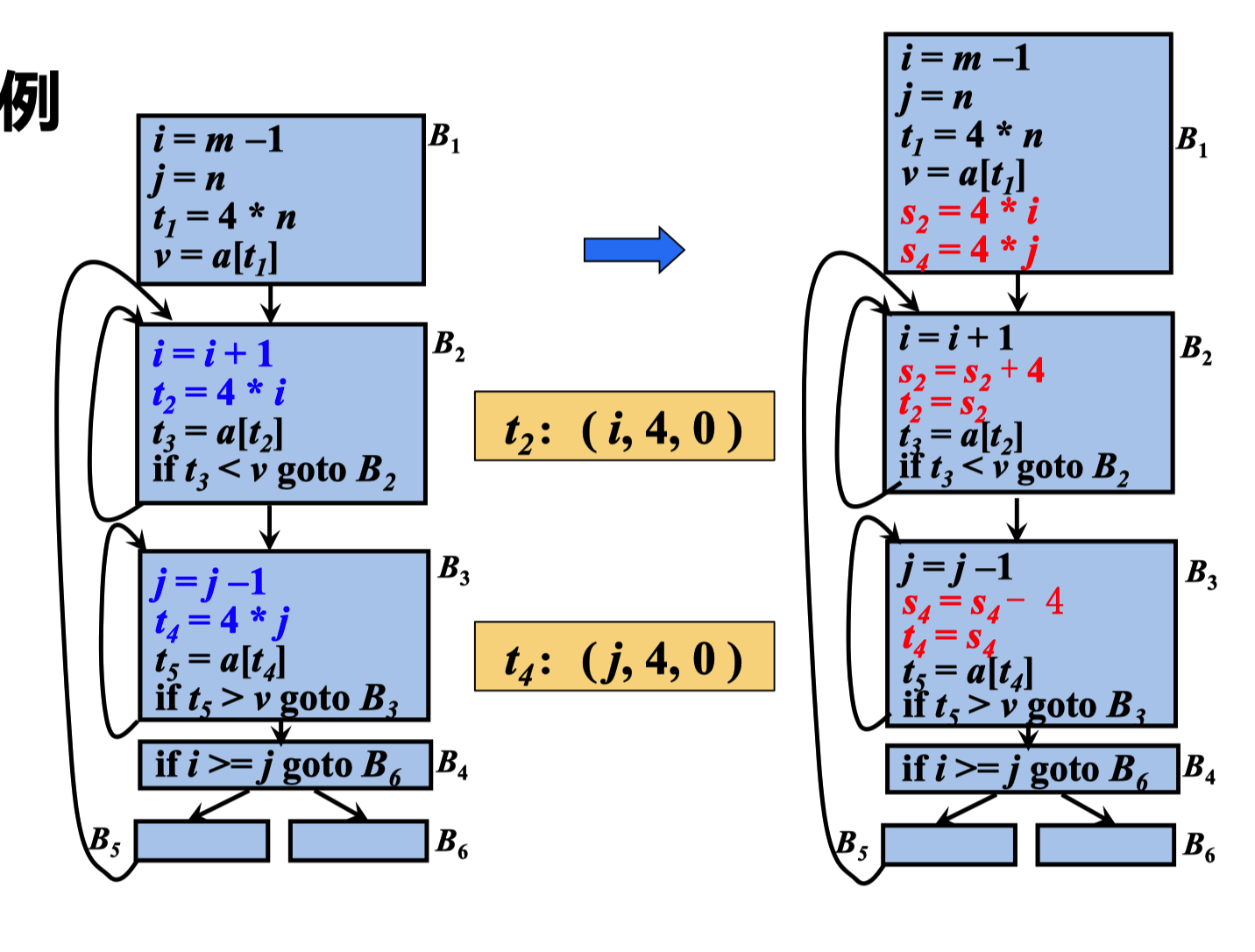
image-20200724112242335

归纳变量的删除

归纳变量的删除

对于在强度削弱算法中引入的复制语句j=t，如果在归纳 变量j的所有引用点都可以用对t的引用代替对j的引用， 并且j在循环的出口处不活跃，则可以删除复制语句j=t

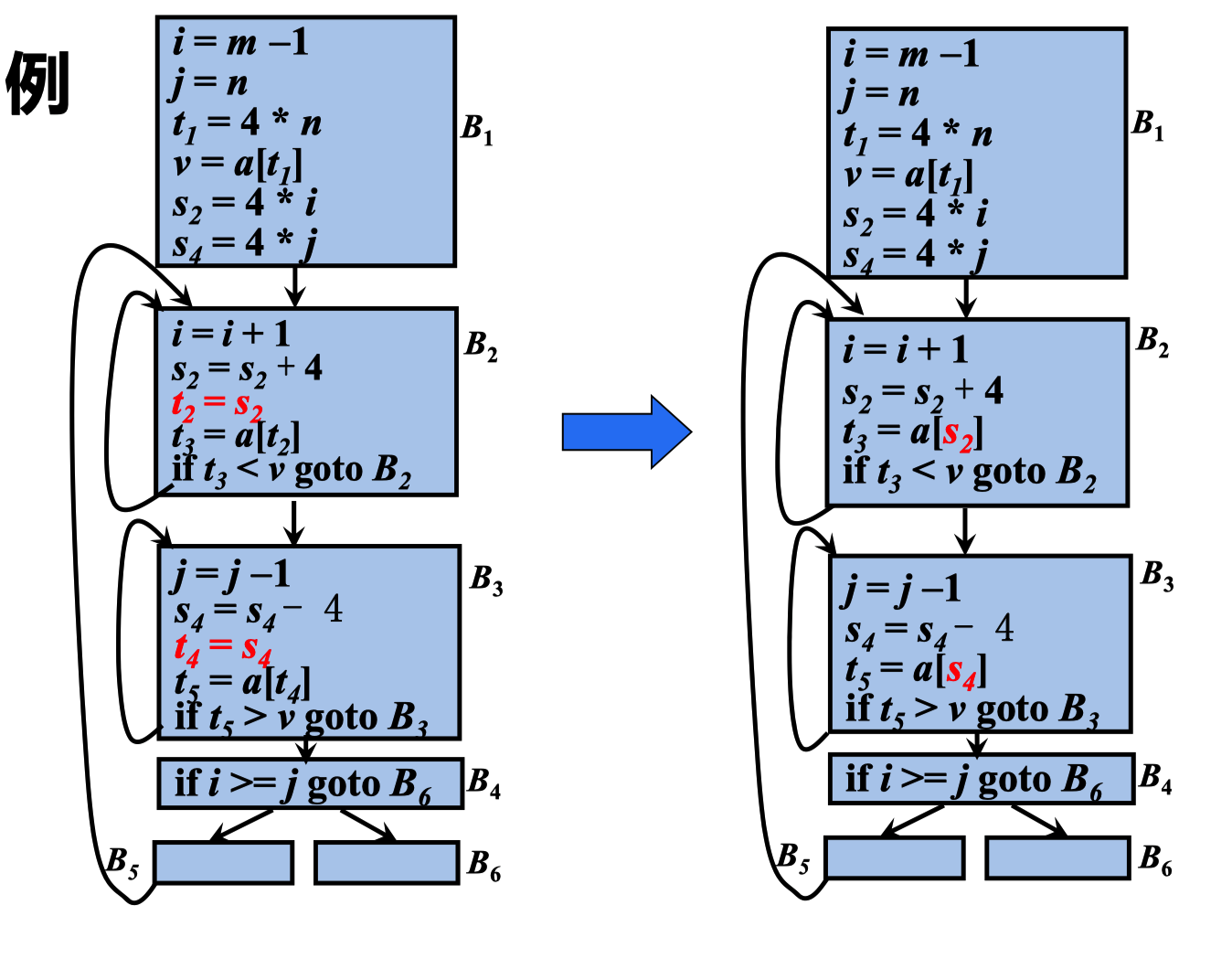image-20200724140831660#

删除仅用于测试的归纳变量

对于仅用于测试的基本归纳变量i，取i族的某个归纳变量j (尽量使得c、d简单，即c=1或d=0的情况)。把每个对i的测 试替换成为对j的测试

  1. ( relop i x B )替换为( relop j c*x+d B )，其中x不是归纳变 量，并假设c>0
  2. ( relop i 1 i 2 B )，如果能够找到三元组j 1 ( i1 , c, d )和j 2 ( i2 , c, d )， 那么可以将其替换为( relop j 1 j 2 B ) (假设c>0 )。否则，测试 的替换可能是没有价值的

如果归纳变量i不再被引用，那么可以删除和它相关的指令

image-20200724140928705
赏

谢谢你请我吃糖果

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

很惭愧<br><br>只做了一点微小的工作<br>谢谢大家